Реферат: Исследование распределения температуры в тонком цилиндрическом стержне
Где k = 0, 1, 2. (2,2)
?? ????????? (2.1) ? (2.2) ????????:
 |
(2.3)
?????
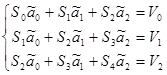 |
??????? (2.3) ?????? ???:
(2.4)
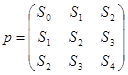 |
? ?????????? ?????????? ???????? Sk ? Vj . ????????? ??????? ????????????? ????????? (2.4) ????? ?p?:
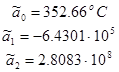 |
??????? ?????? ?????? ??????? (2.4) ? ?????? ???????? ??????? p-1 . ? ?????????? ????????:
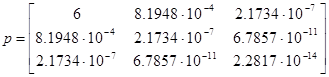 |
?????????? ? (2.1) ????????? ???????? ?????? ????????????? ?к , ??????? ??????????? ???????? ????? S:
Smin =0.7597
При построении доверительных интервалов для оценок коэффициентов определяем предварительно точечные оценки.
??????????????, ??? ????????????????? ???????? xi ???????? ? ???????????? ?????? ????????, ? ????????? ?????? ????????? ???????? Ui ?????????? ? ???????????? ?? ??????????? ?????? ? ?????????? ?????????? s2 , ??????? ??????????. ??? ????????? ???????????????????? Ui ??????????? ????????? ??????????? ?? ???????:
??? r ? ????? ???????? ??????? ???????, ?????? ???????? ????? ??????????? ????????????????? ????? ? ??????????? ??????????? ?????? ?????????????, ?.?. r = 3.
?????? ?????????????? ??????? ????? ???:
?????? ????????? ?????????? ?????? ????????????? ?????? ?? ????????:
Где Sk – минор соответствующего диагонального элемента матрицы нормальной системы;
D - главный определитель нормальной системы.
В нашем случае:
S0 =3.5438 10-22
S1 =-8.9667 10-14
S2 =6.3247 10-7
??????:
????????? ?????? ????????????? ???????????? ?? ??????????? ??????, ?.?. ??????? ??????? ?? ??????? ?????????????? ????????????????? ?????? Ui.
????????, ??? ??? ?????? ??????????? ? ???????????. ????? ????????? ????????:
Имеют распределения Стьюдента, а r = 3.
???????? ????????????? ??????????? b=0,9 ? ?? ??????? ????????? ??????? ??????????? ???????? gb ?????? 2,35, ??????????????? ?????????:
????????????? ????????? ??? ?????????????:
(2.4*)
? ????? ?????? ?????? ???:
2.2 Проверка статистической гипотезы об адекватности модели задачи регрессии.
??????? ??????? ?????? n ????????????????? ???????? (xi ;Ui ). ????????????, ??? ?????? ????????? xi ???????????? ????, ? ????????? ?????? ????????? ?????????? Ui ????????? ??????????? ?????? ? ?????????? ?????????? s2 . ?? ??????? ??????? ????????? ? ????:
???????, ?????? ?? ???? ???????????? ??????????? ??????? ???????, ?.?. ???????? ????:
(2.5)
C ??????? ??? ????? ????? ?????? ???? ??????? ? ??????????? ?????? ????????? ?????????? ????????? Ui ??? ???? ???????:
Где r1 = 4 (количество точек – 6, параметра – 2).
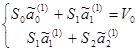 |
?????????? ??????? ????????? ??? ??????????? ????? ?????? ????????????? ??????? (2.5)? ??????? ??? ????? ???:
(2.7)
????? ??? ??????? ??????? ??????, ???????:
(2.8)
Чем лучше функция регрессии описывает эксперимент, тем меньше для неё должна быть оценка дисперсии отдельного измерения Ui, т.к. при плохом выборе функции в дисперсию войдут связанные с этим выбором дополнительные погрешности. Поэтому для того, чтобы сделать выбор между функциями U(x) и U(1)(x) нужно проверить значимость различия между соответствующими оценками дисперсии, т.е. проверить гипотезу:
?0 ? ?????????????? ????????
Т.е. проверить, значимо ли уменьшение дисперсии при увеличении степени многочлена.
? ???????? ???????????? ???????? ?????????? ????????? ????????, ??????:
(2.9)
имеющую распределение Фишера с(r ; r1 ) степенями свободы.Выбираем уровень распределения Фишера, находим критическое значение F* a , удовлетворяющее равенству: p(F>F* a )=a
В нашем случае F=349.02, а F* a =10,13.
???? ?? ??????????? ??????????? ??????????? ??????????? F>Fa , ??????? ??????????? 0,01, ?? ???????? ?0 ???????? ?? ?????????. ?? ? ????? ?????? ????? ???????????? ???????????
, коэффициенты в котором неодинаковы.
3. Нахождение коэффициента теплопроводности a .
 |
??????????? a ???????? ?? ??????? (1.5), ?????????:
(3.1)
????????? ?????????? ?????????? ??????????? ???????? ????????? I, ?????? ?? ??????????, ????? ????????????? ??????????? ?????????? a ?? ???????????? 0,1%, ?.?.:
(3.2)
?.?. ?? (3.1) ????????, ??? a>a0 , ?? ??????? (3.2) ???????? ????? ?????????, ????:
(3.3)
Т.е. в качестве предельно допустимой абсолютной погрешности вычисления интеграла I возьмём d=0,001Т (3.4)
Т=218 о С, следовательно, d=0,218 о С.
3.1 Вычисление интеграла I методом трапеции
Использование теоретической оценки погрешности
??? ??????????? ????????? ???????? ?????????? ?????? n, ?? ??????? ????? ??????? ??????? ?????????????? [0;T] ???????????? ?? ???????:
, где M2 =[f”(t)], t e [0;T], f(t)=e-bt3
???????? ??????? (3.4) ????????:
(3.5)
????????????? f(t), ???????:
? ??????????? ??????? ??????????: f?(t)-f???(t)=0, ?????? ????????:
Далее вычисляем значения f’’(t) при t=t1 , t=t2 , t=0 и t=T, получаем:
f’’(t1)=1.5886 10-4
f’’(t2)=-1.6627 10-4
f’’(0)=0
f’’(T)=7.4782 10-6
Итак: M2 =1,5886 10-4 , откуда n=25.66; принимаем N=26.
 |
????? ???????? ???????? I: