Реферат: Исследование RC-генератора синусоидальных колебаний

GO TO 8

32 HB=2*HB

33 T=T2

DO 35 K=1,N

35 X(K,1)=X(K,3)

KLP=1

GO TO 6

END

4.8Тестовая задача

Решим дифференциальное уравнение

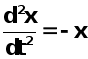
с начальными условиями . Легко видеть, что решением этой задачи является функция . Вычислим решение на интервале , что составит почти периода этой функции. Если при таком длительном интегрировании амплитуда косинусоиды существенно не изменится, то алгоритм численно устойчив. Можно также сравнить решение в конечной точке

Подпрограмма правых частей для этого уравнения будет такой.

SUBROUTINE PRAV(T,X,F,N)

DIMENSION X(N),F(N)

F(1)=X(2)

F(2)= -X(1)

RETURN

END

В подпрограмме вывода предусмотрим заполнение результатами массива D для построения графиков на интервале в пять периодов, а также заполнение массива С положительными максимумами вычисляемой функции на всем интервале интегрирования. Эти массивы передадим в главный модуль через общую область.

SUBROUTINE OUT(T,X,F,N,IER)

DIMENSION X(N),F(N),D(3,1000),C(300)

COMMON K,L,KP,D,C

IF(T.LT.31.4)THEN

K=K+1

D(1,K)=T

D(2,K)=X(1)

D(3,K)=X(2)

ENDIF

IF(X(1).LT.0.AND.KP.EQ.1)THEN