Реферат: Исследование RC-генератора синусоидальных колебаний

Рабочий массив размера (N,3)

Блок-схема алгоритма изображена на Рисунке 2. Номер переменной записан как верхний индекс.

В цикле с номерами блоков 2, 3, 4, 5 обнуляются второй и третий столбцы рабочего массива R.

Внешний цикл с номерами блоков 6 - 18 вычисляет производные в четырех им формируемых точках и накапливает средневзвешенное значение приращений в третьем столбце рабочего массива R. Вдоль столбца расположены значения, соответствующие всем N искомым переменным.

Блок 7 задает в цикле последовательно значения независимой переменной : TN, TN+0.5H, TN+0.5H, TN+H .Константы 0, 0.5, 0.5 и 1 содержатся в первом столбце массива Р.

Цикл 8 - 11 записывает в первый столбец рабочего массива значения переменных для вычисления производных. Для этого к начальному значению переменной прибавляется сначала нулевое приращение, затем половина приращения, получаемого на шаге со значением производной в начальной точке, потом половина приращения, получаемого на шаге с значением производной во второй точке, и , наконец, полное приращение, получаемое на шаге со значением производной в третьей точке.

В блоке 12 выполняется обращение к подпрограмме вычисления производных. Подпрограмме передается значение независимой переменной и первый столбец рабочего массива, содержащий значения зависимых переменных в задаваемой точке. Подпрограмма возвращает массив F значений производных.

В цикле 13 - 16 во второй столбец рабочего массива по вычисленным значениям производных записываются приращения, а в третьем столбце накапливаются суммы четырех приращений с весовыми коэффициентами 1/6, 1/3, 1/3, 1/6 . Константы 6, 3, 3, 6 для этого хранятся во втором столбце массива Р.

В цикле 19 - 22 полученные приращения прибавляются к начальной точке и результат записывается в выходной массив.

В блоке 23 вычисляются производные в конечной точке шага.

4.3Блок - схема алгоритма одного шага по методу Рунге - Кутта

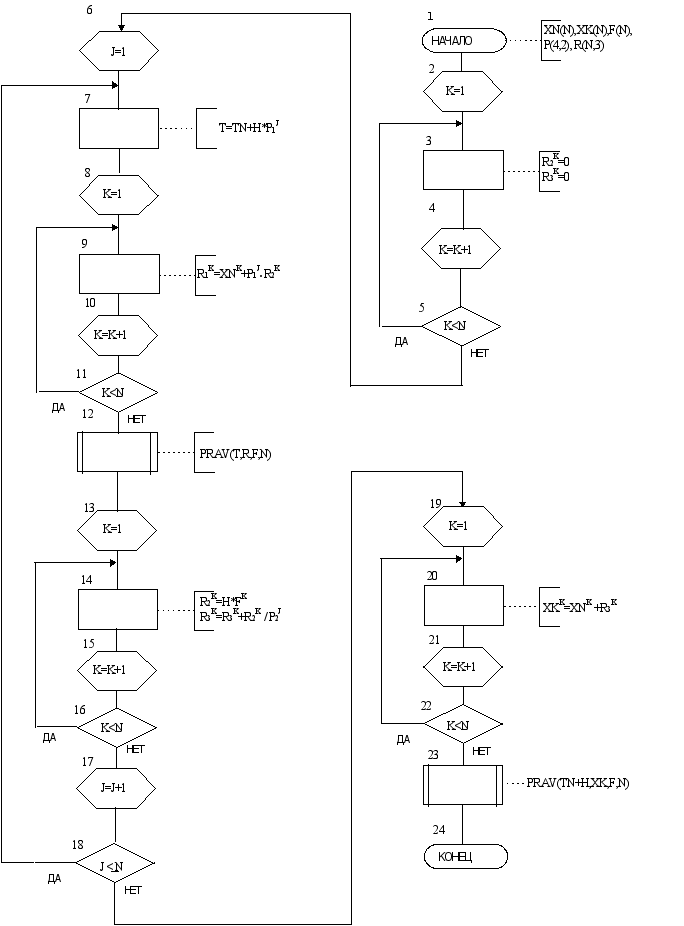
Рисунок 2

4.4Подпрограмма одного шага по методу Рунге-Кутта.

SUBROUTINE SH(TN,H,XN,XK,F,PRAV,N,R)

DIMENSION XN(N),XK(N),F(N),P(4,2),R(N,3)

DATA P/0.,.5,.5,1.,6.,3.,3.,6./

DO 1 K=1,N

R(K,2)=0.

1 R(K,3)=0.

DO 4 J=1,4 ! Начало внешнего цикла определения 4-х приращений

T=TN+P(J,1)*H ! Задание независимой переменной.

DO 2 K=1,N ! Цикл задания массива значений зависимых переменных.

2 R(K,1)=XN(K)+P(J,1)*R(K,2)

CALL PRAV(T,R,F,N) ! Вычисление производных в заданной точке.

DO 3 K=1,N ! Цикл вычисления и накопления частичных приращений.

R(K,2)=H*F(K)

3 R(K,3)=R(K,3)+R(K,2)/P(J,2)

4 CONTINUE

DO 5 K=1,N

5 XK(K)=XN(K)+R(K,3) ! Вычисление переменных в конечной точке.