Реферат: Исследование RC-генератора синусоидальных колебаний

2,75

2,4

1,73

1

0,02

-1

-1,73

-2,4

-2,75

-3

3.ФУНКЦИОНАЛЬНОЕ ПРОЕКТИРОВАНИЕ ПРОГРАММНОГО КОМПЛЕКСА

Функционально программный комплекс должен состоять из двух независимых частей:

• программы - модели RC - генератора;

• набора программ обработки результатов моделирования автогенератора.

Модель RC - генератора должна, в свою очередь, включать:

• модуль, вызывающий подпрограмму метода Рунге - Кутта;

• модули метода Рунге - Кутта;

• модуль - модель усилителя;

• модуль правых частей ;

• модуль вывода результатов одного шага интегрирования.

Для программной реализации метода Рунге - Кутта удобно использовать два модуля:

• модуль, выполняющий один заданный шаг метода;

• модуль, управляющий величиной шага в зависимости от получаемой погрешности решения.

Взаимодействие этих модулей таково. Вызывающий модуль вводит значение параметра , начало и конец интервала интегрирования, максимальный шаг, начальные условия и заданную погрешность. Затем этот модуль обращается к модулю управления метода Рунге - Кутта. Последний задает величину шага подпрограмме одного шага и ведет процесс интегрирования системы уравнений, удерживая погрешность в заданных пределах. При выполнения шага, в соответствие с методом Рунге - Кутта, модуль шага четырежды обращается к модулю правых частей, а тот, в свою очередь, - к модели усилителя в виде функции . После выполнения шага, удовлетворяющего условиям точности, модуль управления вызывает подпрограмму вывода результатов шага, а она, в свою очередь обращается к модели усилителя в виде функции . Модуль управления заканчивает свою работу после достижения конца интервала интегрирования. Тогда вызывающий модуль обращается к подпрограмме вывода таблиц и графиков KRIS.

В набор подпрограмм обработки результатов моделирования необходимо включить две независимые программы:

• программу численного интегрирования по методу трапеций;

• программу аппроксимации экспериментальных зависимостей степенными многочленами методом наименьших квадратов.

4.МОДУЛИ РЕШЕНИЯ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

4.1 Описание метода Рунге - Кутта четвертого порядка

Сначала рассмотрим применение метода для решения дифференциального уравнения, а затем для случая системы уравнений.

Пусть имеется уравнение

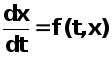или