Реферат: Исследование RC-генератора синусоидальных колебаний
- неизвестная функция от независимой переменной 
;
- известная функция.
Все численные методы решения задачи Коши основаны на приближенной замене искомой функции степенными многочленами.
В методе Рунге-Кутта четвёртого порядка отыскивается приращение, которое даёт приближающий многочлен на шаге интегрирования. Приращение искомой функции вычисляется в виде произведения длины шага на значение производной от этой функции. В качестве производной берется средневзвешенное от значений производных 
вычисленных в специально подобранных четырёх точках.
В качестве первой точки берут начальную точку шага 
.
Производная в этой точке равна
,
где - правая часть уравнения .
В качестве второй точки на плоскости решения 
выбирают точку с координатами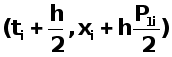 
.
Производная во второй точке равна
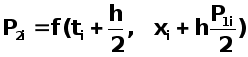
Для третьей точки берут координаты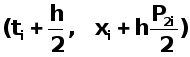 
и вычисляют производную
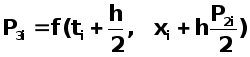
Наконец, для четвёртой точки берут координаты 
и вычисляют производную
По полученным четырём значениям производной находят средневзвешенное значение
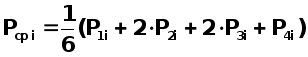
Теперь, находят координаты конечной точки шага.
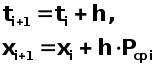
При решении системы уравнений вычисления ведут параллельно для каждого из уравнений.
4.2Описание алгоритма одного шага
В алгоритме используются следующие идентификаторы
Таблица 4
|
Имя |
Тип |
Назначение |
|
PRAV |
Подпрограмма. |
Подпрограмма, возвращающая значения производных. |
|
N |
К-во Просмотров: 647
Бесплатно скачать Реферат: Исследование RC-генератора синусоидальных колебаний
|