Реферат: Исследование спектров немодулированных и модулированных колебаний и сигналов

В соответствие с формулой Фурье изменение формы сигнала при модуляции приводит к изменению спектра модулированного сигнала. Чем выше максимальная частота спектра модулирующего сигнала , тем шире спектр модулированного сигнала.

Количественное значение увеличения ширины спектра этого сигнала зависит от вида модуляции и ширины спектра модулирующего сигнала.

Ширина спектра модулированного синусоидального сигнала составляет:

-для АМ: ∆F_АМ = 2F_с.м. ;

-для ЧМ: ∆F _ЧМ >> F_с.м. ;

-для ФМ: ∆F_ФМ ≈ ∆F_ЧМ ;

Для радиовещания ширина спектра для ЧМ сигнала составляет 100÷150 кГц, а для АМ»7 кГц.

Любое сообщение в общем случае можно описать с помощью трех основных параметров:

-динамическим диапазоном – Д_с ;

-шириной спектра частот - ∆F_с ;

-длительностью передачи – t_c ;

Произведение Д_{с *} ∆F_{с *} t_c = V_c называется объемом сигнала. (рис 5)

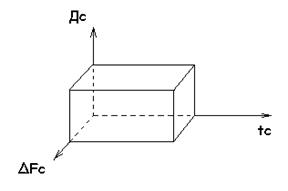
Рис. 5. Графическое представление объема сигнала

Для обеспечения неискаженной передачи сообщения объемом V_c , необходимо чтобы характеристики среды распространения и непосредственно приемника соответствовали ширине спектра и динамическому диапазону.

Для безискаженной передачи сообщения в реальном масштабе времени полоса пропускания приемника должна соответствовать ширине спектра сигнала.

Проблема передачи информации, содержащейся во многих низкочастотных сигналах, с помощью множества узкополосных каналов связи с разными частотами решается при использовании модулированных сигналов.

Модулированный сигнал – это узкополосный сигнал, параметры которого изменяются пропорционально низкочастотному информационному сигналу. Модулированный сигнал, как правило, является высокочастотным колебанием.

Для получения модулированного сигнала используется гармоническое (несущее) колебание (несущая частота).

Информация вносится в несущее колебание с использованием модуляции – изменение какого-либо из параметров высокочастотного колебания пропорционально низкочастотному сигналу .

Амплитудная модуляция (АМ).

При АМ амплитуда сигнала меняется пропорционально низкочастотному информационному сигналу: , где - начальное значение амплитуды несущей; k_AM - коэффициент амплитудного модулятора.

Поэтому сигнал с АМ: .

Пусть сообщение , тогда

,

где - коэффициент амплитудной модуляции, основной параметр АМ – колебаний с гармонической модуляцией.

Используя тригонометрическую формулу для произведения косинусов, получим:

Все три слагаемых – гармонические колебания: первое – несущее колебание, второе и третье слагаемые называют соответственно верхней и нижней боковыми составляющими. Таким образом, эта формула дает полное спектральное разложение АМ колебания (амплитудный и фазовый спектры). Ширина амплитудного спектра этого АМ - колебания равна (2W) удвоенной частоте модулирующего сигнала.

Если модуляция осуществляется сплошным периодическим сигналом, в спектре которого содержатся много гармоник, то каждая из них даст две боковые составляющие в спектре модулированного сигнала. В спектре появляется верхняя и нижняя боковые полосы. Ширина спектра будет определяться модулирующей гармоникой с максимально высокой частотой. Обе боковые полосы несут полную информацию о н\ч модулирующем сигнале. Поэтому в технике связи часто используются сигналы с одной боковой полосой (ОБП- сигналы).

Амплитудно-импульсная модуляция (АИМ)