Реферат: Изгиб бруса

или

(28)

Здесь M – момент сил и относительно начала координат :

(29)

и – поперечные силы в направлении осейи :

(30)

(31)

Если брус изгибается только силой , параллельной главной цен­тральной оси то равенство (28) принимает вид:

(32)

Учитывая выражения (18) для и формуле (29) можно при­дать вид

Первый интеграл в последнем равенстве преобразуем с учетом:

Тогда в случае односвязного (сплошного) поперечного сечения имеем:

(33)

Формулы (32) и (33) позволяют определить координату цент­ра изгиба, когда брус изгибается силой , линия действия которой параллельна главной плоскости .

Центр изгиба всегда расположен на оси симметрии сечения. Если сечение имеет две оси симметрии, то центр изгиба совпадает с точкой их пересечения, т. е. с центром тяжести сечения.

ГЛАВА III

Частные случаи задачи об изгибе бруса

§ 1. ИЗГИБ БРУСА ЭЛЛИПТИЧЕСКОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Рассмотрим поперечный изгиб консольного бруса силами, распре­деленными на его торце и приводящимися к силе , направленной по оси (рис.5)

Рис.5

Контур эллиптического поперечного сечения определяется урав­нением:

(34)

На основании (19) функция напряжений на контуре сечения обращается в нуль:

(35)

если произвольная функция

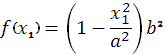(36)

Уравнение (26) с учетом выражения (36) для функции принимает вид: