Реферат: Изгиб бруса

(58)

На основании мембранной аналогии правая часть уравнения (57) пропорциональна нагрузке на мембрану, равномерно натянутую на жесткий полукруглый контур. Это обстоятельство позволяет заклю­чить, что функция напряжений должна быть четной относительно координаты , поэтому будем искать ее в следующем виде:

(59)

Ссылаясь на (57), убеждаемся, что

(

поэтому подстановка выражения (59) для функции в уравнение (57) дает

Отсюда находим, что при постоянных:

(60)

выражение (59) для функ­ции удовлетворяет урав­нению (57).Обратимся к граничным условиям для функции Ф. Очевидно, что на прямо­линейном участке кон­тура ( ) условие (56) выполняется только при нечетных значе­ниях

Следовательно, выраже­ние (59) на полуокружно­сти контура (принимает вид:

,

а чтобы удовлетворялось условие (55), необходимо

(61)

Для определения коэффициентов ряда равенства (61) умножим последнее на и проинтегрируем в пределах от .

Учитывая, что

и

Находим

(62)

Тогда выражение (59) для функции напряжений принимает

вид:

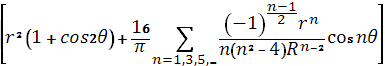* (63)

Определим координату центра изгиба. Для этого предвари­тельно вычислим момент по формуле (33), которая c учетом выра­жения (63) приводится к виду:

Поскольку , то