Реферат: Хеширование

25

Volatile

31

Do

14

If

16

Static

6

While

11

Подробный анализ алгоритма, а также реализацию на С++ можно найти по адресу [12]. Там же описываются методы разрешения коллизий. К сожалению, эта тема выходит за рамки этой работы.

Разрешение коллизий

Составление хеш-функции – это не вся работа, которую предстоит выполнить программисту, реализующему поиск на основе хеширования. Кроме этого, необходимо реализовать механизм разрешения коллизий. Как и с хеш-функциями существует несколько возможных вариантов, которые имеют свои достоинства и недостатки.

Метод цепочек

Метод цепочек – самый очевидный путь решения проблемы. В случае, когда элемент таблицы с индексом, который вернула хеш-функция, уже занят, к нему присоединяется связный список. Таким образом, если для нескольких различных значений ключа возвращается одинаковое значение хеш-функции, то по этому адресу находится указатель на связанный список, который содержит все значения. Поиск в этом списке осуществляется простым перебором, т.к. при грамотном выборе хеш-функции любой из списков оказывается достаточно коротким. Но даже здесь возможна дополнительная оптимизация. Дональд Кнут ([3], стр. 558) отмечает, что возможна сортировка списков по времени обращения к элементам. С другой стороны, для повышения быстродействия желательны большие размеры таблицы, но это приведет к ненужной трате памяти на заведомо пустые элементы. На рисунке ниже показана структура хеш-таблицы и образование цепочек при возникновении коллизий.

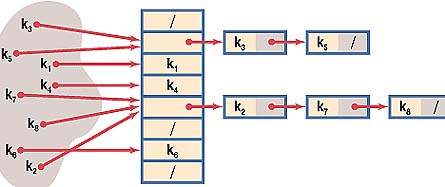
Прекрасная наглядная иллюстрация этой схемы разрешения коллизий в виде Java-апплета вместе с исходным кодом на C++ представлена по адресу [14].

Открытая адресация

Другой путь решения проблемы, связанной с коллизиями, состоит в том, чтобы полностью отказаться от ссылок, просто просматривая различные записи таблицы по порядку до тех пор, пока не будет найден ключ K или пустая позиция [3]. Идея заключается в формулировании правила, согласно которому по данному ключу определяется «пробная последовательность», т.е. последовательность позиций таблицы, которые должны быть просмотрены при вставке или поиске ключа K. Если при поиске встречается пустая ячейка, то можно сделать вывод, что K в таблице отсутствует, т.к. эта ячейка была бы занята при вставке, т.к. алгоритм проходил ту же самую цепочку. Этот общий класс методов назван открытой адресацией [4].

Линейная адресация

Простейшая схема открытой адресации, известная как линейная адресация (линейное исследование, linear probing) использует циклическую последовательность проверок

h(K), h(K - 1), …, 0, M – 1, M – 2, …, h(K) + 1

и описывается следующим алгоритмом ([3], стр. 562). Он выполняет поиск ключа K в таблице из M элементов. Если таблица не полна, а ключ отсутствует, он добавляется.

Ячейки таблицы обозначаются как TABLE[i], где 0 ≤ i < M и могут быть или пустыми, или занятыми. Вспомогательная переменная N используется для отслеживания количества занятых узлов. Она увеличивается на 1 при каждой вставке.

1. Установить i = h(K)
2. Если TABLE[i] пуст, то перейти к шагу 4, иначе, если по этому адресу искомый, алгоритм завершается.
3. Установить i = i – 1, если i < 0, то i = i +M. Вернуться к шагу 2.
4. Вставка, т.к. поиск оказался неудачным. Если N = M – 1, то алгоритм завершается по переполнению. Иначе увеличить N, пометить ячейку TABLE[i] как занятую и установить в нее значение ключа K.

Опыты показывают ([3], стр. 564), что алгоритм хорошо работает в начале заполнения таблицы, однако по мере заполнения процесс замедляется, а длинные серии проб становятся все более частыми.

Квадратичная и произвольная адресация

Вместо постоянного изменения на единицу, как в случае с линейной адресацией, можно воспользоваться следующей формулой [15]

h = h + a² ,

где a – это номер попытки. Этот вид адресации достаточно быстр и предсказуем (он проходит всегда один и тот же путь по смещениям 1, 4, 9, 16, 25, 36 и т.д.). Чем больше коллизий в таблице, тем дольше этот путь. С одной стороны, этот метод дает хорошее распределение по таблице, а с другой занимает больше времени для просчета.

Произвольная адресация использует заранее сгенерированный список случайных чисел для получения последовательности [15]. Это дает выигрыш в скорости, но несколько усложняет задачу программиста.

Адресация с двойным хешированием