Реферат: Классификация систем массового обслуживания и их основные элементы

т.е. при 1

(10)

и при

(11)

Введём для удобства записи обозначение

.

Уравнение (10) позволяет заключить, что при 1

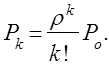(12)

При из (11) находим, что

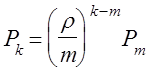
и, следовательно, при

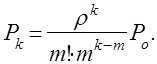(13)

Остаётся найти . Для этого в (9) подставляем выражения из (12) и (13). В результате

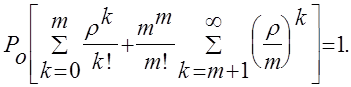
так как бесконечная сумма, стоящая в квадратных скобках, сходится только при условии, что

(14)

то при этом предположении находим равенство

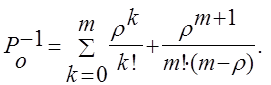(15)

Если условие (14) не выполнено, т.е. если , то ряд, стоящий в квадратнойскобке уравнения для определения , расходится и, значит, должно быть равно 0. Но при этом, как следует из (12) и (13), при всех оказывается .

Методы