Реферат: Кластерный анализ в портфельном инвестировании

Теперь вводится в полученное уравнение регрессии второй фактор таким образом, чтобы значение R-квадрат снова оказалось максимально возможным, и затем рассчитываем второй коэффициент последовательной детерминации:

[1,стр.147]

Аналогичным образом рассчитываем следующие коэффициенты:

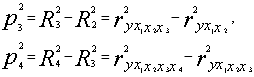и т.д. [1,стр.147]

Базовый отбор факторов продолжается до тех пор, пока величина получаемых коэффициентов последовательной детерминации не станет меньше некоторого критического значения. Учитывая, что в механизм расчета скорректированной величины R-квадрат входит поправка на возрастание энтропии при вводе новых факторов, ее прирост на каждой итерации алгоритма должен быть положительным и, следовательно, критическое значение p должно быть больше нуля.

Данный метод позволяет отобрать из всех имеющихся факторов именно те, которые оказывают наибольшее влияние на доходность рассматриваемых ценных бумаг. Это позволяет существенно понизить размерность модели, создаваемой на основе методики, ускорить вычисления и при этом отбросить данные, не имеющие большого влияния на интересующие нас показатели. Как правило, от выявленных главных компонент зависит не менее 85% общей дисперсии, что лишний раз показывает эффективность выбранного метода анализа.

Теперь, когда определены методы отбора факторов и технология разбиения множества ценных бумаг на отдельные кластеры, можно приступать непосредственно к построению методики оптимизации инвестиционного портфеля. Учитывая, что в настоящее время внедрение любой экономической методики немыслимо без автоматизации, существует алгоритм, по которому надлежит производить операции для получения искомого результата: оптимизированного набора ценных бумаг, позволяющих получить максимальную прибыль при заданном уровне риска.

На первом этапе определяются исходные массивы данных, которые подлежат математической обработке.

В начале имеются следующими исходными данными: S₁ , S₂ , ..., S_N – рассматриваемое множество ценных бумаг;

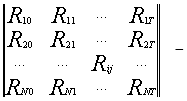[1,стр.149]

матрица доходности ценных бумаг S₁ -S_N за периоды [0 ; T ],

где R_ij – доходность по ценной бумаге i за j -й период;

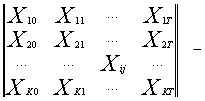[1,стр.151]

матрица факторов X₁ -X_K за периоды [0 ; T ],

где X_ij – значение фактора X_i за j -й период;

s _п – оценка риска предполагаемого портфеля ценных бумаг.

Теперь необходимо определить доли m₁ , ..., m_N имеющихся в инвестиционном портфеле ценных бумаг с целью максимизации доходности в следующем периоде при заданном уровне риска:

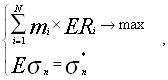[1,стр.153]

где уровень доходности R_i вычисляется как отношение ожидаемой в отчетный период стоимости ценной бумаги S_i к курсовой стоимости в момент формирования портфеля за вычетом единицы.

Так, доходность за месяц в момент времени t =1 вычисляется следующим образом:

[1,стр.155]

В случае, когда инвестор не имеет возможностей продавать ценные бумаги без покрытия, вводится дополнительное условие: m_y >0 , где y – номер соответствующей ценной бумаги.

Вывод: принято группирование ценных бумаг на основе существующих индустриальных и прочих классификаций.

3. Алгоритм оптимизации портфеля с применением кластерного анализа

Предлагаемый алгоритм можно условно разбить на четыре основные стадии:

1) Разбиение множества ценных бумаг на отдельные кластеры;

2) Определение факторов, влияющих на доходность составляющих каждого кластера. Расчет факторных весов. Построение уравнения регрессии;

3) Прогнозирование динамики выбранных факторов;

4) Вычисление ожидаемой доходности и степени риска для каждой ценной бумаги;