Реферат: Коды Фибоначи Коды Грея
Такое представление чисел N называется p -кодом Фибоначчи. Каждому p Î{ 0, 1, 2, …, ¥} соответствует свой код, т. е. их число бесконечно.
При p = 0 p -код Фибоначчи совпадает с двоичным кодом.
Для 1-кода Фибоначчи кодовые комбинации имеют вид:
Таблица 2
|
N | KK | Вес порядка | |||||
| 5 | 4 | 3 | 2 | 1 | |||
| 0 | A0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | A1 | 0 | 0 | 0 | 0 | 1 | |
| 1 | A2 | 0 | 0 | 0 | 1 | 0 | |
| 2 | A3 | 0 | 0 | 0 | 1 | 1 | |
| 2 | A4 | 0 | 0 | 1 | 0 | 0 | |
| 3 | A5 | 0 | 0 | 1 | 0 | 1 | |
| 3 | A6 | 0 | 0 | 1 | 1 | 0 | |
| 4 | A7 | 0 | 0 | 1 | 1 | 1 | |
| 3 | A8 | 0 | 1 | 0 | 0 | 0 | |
| 4 | A9 | 1 | 0 | 0 | 0 | 1 | |
| 4 | A10 | 0 | 1 | 0 | 1 | 0 | |
| 5 | A11 | 0 | 1 | 0 | 1 | 1 | |
| 5 | A12 | 0 | 1 | 1 | 0 | 0 | |
| 6 | A13 | 0 | 1 | 1 | 0 | 1 | |
| 6 | А14 | 0 | 1 | 1 | 1 | 0 | |
| 7 | А15 | 0 | 1 | 1 | 1 | 1 | |
| N | KK |
Вес порядка | |||||
| 5 | 4 | 3 | 2 | 1 | |||
| 5 | A16 | 1 | 0 | 0 | 0 | 0 | |
| 6 | A17 | 1 | 0 | 0 | 0 | 1 | |
| 6 | А18 | 1 | 0 | 0 | 1 | 0 | |
| 7 | A19 | 1 | 0 | 0 | 1 | 1 | |
| 7 | A20 | 1 | 0 | 1 | 0 | 0 | |
| 8 | A21 | 1 | 0 | 1 | 0 | 1 | |
| 8 | A22 | 1 | 0 | 1 | 1 | 0 | |
| 9 | A23 | 1 | 0 | 1 | 1 | 1 | |
| 8 | A24 | 1 | 1 | 0 | 0 | 0 | |
| 9 | A25 | 1 | 1 | 0 | 0 | 1 | |
| 9 | A26 | 1 | 1 | 0 | 1 | 0 | |
| 10 | A27 | 1 | 1 | 0 | 1 | 1 | |
| 10 | A28 | 1 | 1 | 1 | 0 | 0 | |
| 11 | A29 | 1 | 1 | 1 | 0 | 1 | |
| 11 | A30 | 1 | 1 | 1 | 1 | 0 | |
| 12 | А31 | 1 | 1 | 1 | 1 | 1 | |
Как видно из таблицы 5 разрядным 1-кодом Фибоначчи можно закодировать 13 натуральных чисел от 0 до 12, при этом каждому числу соответствует множество комбинаций.
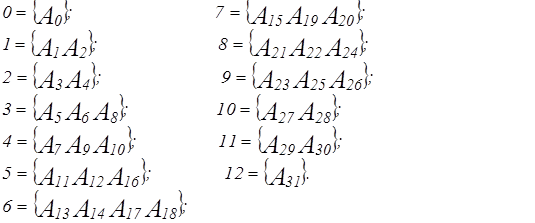
Коды Фибоначчи образуют соответствующую систему счисления с набором арифметических операций.
Сложение: Вычитание:
0+0 = 0; 0- 0 = 0;
0+1 = 1; 1 -1 = 0;
1+0 = 1; 1 -0 = 1;
1+1 = 111; 10-1 = 1;
1+1 = 1001; 110 -1 = 11;
1000-1 = 111.
При сложении 2-х единиц может быть:
1. j 1 (n)+ j 1 (n)= j 1 (n)+ j 1 (n-1)+ j 1 (n-2) т. е. равно 1 и перенос 1 в два младших разряда.
2. j 1 (n)+ j 1 (n)= j 1 (n+1)+ j 1 (n-2) т. е. равно 0 и перенос 1 в два разряда - предыдущий и последующий.
Коды Фибоначчи обладают рядом полезных свойств (например, избыточность и т. д.), позволяющих строить быстродействующие и помехоустойчивые АЦП (“фибоначчевые” АЦП), реализующих специальные алгоритмы преобразования. Коды Фибоначчи используются для диагностики ЭВМ, в цифровых фильтрах для улучшения спектрального состава сигнала за счет перекодировки и др. областях.
2. ДВОИЧНЫЙ ОТРАЖЕННЫЙ КОД. КОД ГРЕЯ
Код Грея отличается от двоичного кода тем, что при переходе к следующей кодовой комбинации изменяется только один элемент кодовой комбинации (табл. 3).
Если при передаче сообщений с помощью кода Грея одновременно изменяется несколько разрядов кода, то это свидетельствует об ошибке, в этом состоит обнаруживающая способность кода Грея.
Код Грея, не взвешенный и непригоден для вычислительных операций без предварительного перевода в двоичный код.
|