Реферат: Коды Фибоначи Коды Грея

В математике существует большое количество иррациональных (несоизмеримых) чисел, т. е. обозначающих длину отрезка несоизмеримого с единицей масштаба. Ряд из них широко используется как в математике, так и в др. областях.

Например: Число p = 2 p R/D=3,14159 … , которое представляет отношение длины окружности к ее диаметру. Число e = 2,71828 … , при этом 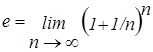. Логарифмы с основанием e удобны для математических расчетов. Число Ö 2 =1,44 … , которое представляет отношение диагонали к стороне квадрата и ряд других чисел.

Особое иррациональное число a = (1+ Ö 5)/2 = 1,61803, которое называется золотая пропорция или золотое сечение и является результатом решения задачи деления отрезка в крайнем и среднем отношении (рис. 1)

A C B

о o o

Рис. 1 Деление отрезка

Если задан отрезок AB то необходимо найти такую точку C , чтобы выполнялось условие AB/CB = CB/AC.

Обозначим: x = CB/AC ; (CB+AC)/CB = 1+1/x = x .

При этом x² –x–1 = 0 . Корни этого уравнения равны: x_1,2 =(1 ± Ö 5)/2 .

Положительный корень называется золотой пропорцией , а точка C - золотым сечением. Золотая пропорция обладает рядом уникальных свойств.

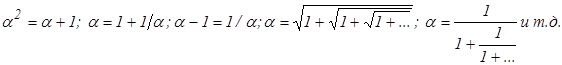
Пропорция 1,61... использовалась в архитектуре, художественных произведениях, музыке с античных времен. С этим числом связан ореол мистики, таинственности, божества и т.д.

В последнее десятилетие эта пропорция нашла свое применение в ЭВМ, АЦП-ЦАП, измерениях и т. д.

1.2 ЧИСЛА ФИБОНАЧЧИ

С золотым сечением тесно связаны числа Фибоначчи открытые итальянским математиком Леонардо из Пизы (Фибоначчи) в XIII веке, которые вычислены по формуле:

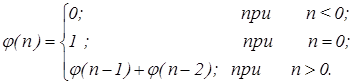(1)

Эти числа представляют ряд: 1, 1, 2, 3, 5, 8, 13, 21...

Отношение соседних чисел Фибоначчи 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13 ... в пределе стремится к золотой пропорции

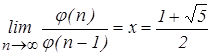. (2)

Числа Фибоначчи обладают еще рядом полезных свойств. Например, остатки от деления чисел Фибоначчи на 2 образуют последовательность: 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, ... и т. д.

Обобщенные числа Фибоначчи или p -числа Фибоначчи вычисляются по рекуррентной формуле:

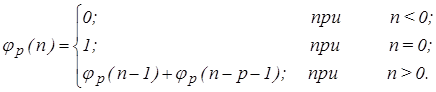(3)

Где p = 0, 1, 2, 3, … . При р = 0 число j ₀ (n) совпадает с двоичными разрядами 2ⁿ (табл. 1).

Таблица 1

n	0	1	2	3	4	5
j 0 (n)	1	2	4	8	16	32

При р = 1 число j ₀ (n) совпадает с обычным рядом Фибоначчи:

1, 1, 2, 3, 5, 8, ...

При р = число j ₀ (n) = 1 для любого n ³ 0 равно:

1, 1, 1, 1, 1, 1, 1, 1, ...

1.3 КОДЫ ФИБОНАЧЧИ

Любое натуральное число N можно представить с помощью p -чисел Фибоначчи

(4)

где: a_i Î{0, 1} - двоичная цифра i -го разряда; j _p (i) - вес i -го разряда;

Любое натуральное число N можно представить также следующим способом:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--