Реферат: Компактные операторы

3) ;

4) ;

([1], стр. 120).

Примеры линейных пространств

1. Пространство действительных чисел является линейным пространством по операциям сложения и умножения.

2. – пространство, элементами которого являются последовательности чисел , удовлетворяющих условию 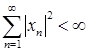с операциями ,

([1], стр. 121).

1.2 Нормированные пространства

Определение: Множество называется нормированным пространством, если:

1) – линейное пространство над полем действительных или комплексных чисел.

2) Для каждого элемента определено вещественное число, называемое его нормой и обозначаемое , и выполнены условия:

а) для любого ;

б) для любого и любого ;

в) , для любых

([1], стр. 138).

Примеры нормированных пространств:

1. Пространство становится нормированным, если положить .

2. Пространство с элементами нормировано, при условии .

3. Пространство функций, непрерывных на отрезке , нормировано, если взять .

([1], стр. 139).

1.3 Банаховы пространства

Определение: Расстоянием (метрикой) между двумя элементами и называется вещественное неотрицательное число, обозначаемое и подчиненное трем аксиомам:

1) ;

2) ;

3) ;

Определение: Последовательность точек метрического пространства называется фундаментальной, если при .

Справедливы утверждения:

1. Если последовательность сходится к некоторому пределу, то она фундаментальна.

Доказательство: