Реферат: Компьютерное математическое моделирование в экономике

1) была бы точно удовлетворена потребность в стали предприятий Q₁ , Q₂ ,..., Q_k ;

2) была бы вывезена вся сталь с заводов P_I , Р₂ , ..., Р_т ;

3) общая стоимость перевозок была бы наименьшей.

Обозначим через Х_ij количество стали (в тоннах), предназначенной к отправке с завода Р_i на предприятие Q_J . План перевозок состоит из (m×k) неотрицательных чисел x_ij (i = 1, 2, ..., m; j = 1, 2, ..., k).

Таблица 7.10

Схема перевозок стали

В	В	В	¼	В	Отправлено
Из				…
Из				…
…	…	…	…	…	…	…
Из			xm3	…
Привезено				…

Первое условие примет вид

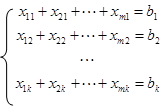(7.74)

Второе условие примет вид

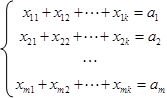(7.75)

Раз стоимость перевозки одной тонны из Р_i , в Q_J равна с_{i j,} то общая стоимость S всех перевозок равна

(7.76)

Таким образом, мы приходим к следующей чисто математической задаче: дана система m+k линейных алгебраических уравнений (7.74) и (7.75) с m·k неизвестны­ми (обычно m·k » m+k) и линейная функция S. Требуется среди всех неотрица­тельных решений данной системы найти такое, при котором функция S достигает наименьшего значения (минимизируется).

Практическое значение этой задачи огромно, ее умелое решение в масштабах нашей страны могло бы экономить ежегодно огромные средства.

Пример 3. Задача о диете. Пусть у врача-диетолога имеется n различных продук­тов F₁ , F₂ , ..., F_n , из которых надо составить диету с учетом их питательности. Пусть для нормального питания человеку необходимо m

веществ N₁ , N₂ , …, N_m . Предположим, что за месяц каждому человеку необходимо g₁ кг вещества N₁ , g₂ кг вещества N₂ , ..., g_m кг вещества N_m . Для составления диеты необходимо знать содержание питательных веществ в каждом продукте. Обозначим через a_ij количе­ство i-го питательного вещества, содержащегося в одном килограмме j-го продукта. Всю эту информацию представляют в виде, так называемой, матрицы питательно­сти (табл. 7.11).

Таблица 7.11

Матрица питательности

Питательное вещество	Продукт
			…
			…
			…
…	…	…	…	…
			…

Предположим, что диетолог уже выбрал диету, т.е. определил, что человек дол­жен за месяц потреблять h₁ кг продукта F₁ ,...,h_n кг продукта F_n . Полное количество питательного вещества N₁ будет

По условию требуется, чтобы его, по крайней мере, хватило

(7.77)

Точно то же и для остальных веществ. В целом

(I = 1, 2, …, m).

(7.78)

Эти условия определяют наличие минимума необходимых питательных веществ. Диета, для которой выполнены условия (7.78) - допустимая диета. Предположим, что из всех допустимых диет должна быть выбрана самая дешевая. Пусть p_i - цена 1 кг продукта F_i . Полная стоимость диеты, очевидно,

(7.79)

Таким образом, мы пришли к задаче: найти неотрицательное решение h₁ , ..., h_n системы неравенств (7.78), минимизирующее выражение (7.79).

В примерах, приведенных выше, имеется нечто общее. Каждый из них требует нахождения наиболее выгодного варианта в определенной экономической ситуа­ции. С чисто математической стороны в каждой задаче требуется найти значение нескольких неизвестных так, чтобы

1) все эти значения были неотрицательны;

2) удовлетворяли системе линейных уравнений или линейных неравенств;

3) при этих значениях некоторая линейная функция имела бы минимум (или мак­симум). Таким образом, линейное программирование - это математическая дисцип­лина, изучающая методы нахождения экстремального значения линейной функции нескольких переменных при условии, что последние удовлетворяют конечному числу линейных уравнений и неравенств. Запишем это с помощью формул: дана система линейных уравнений и неравенств.

Запишем это с помощью формул: дана система линейных уравнений и неравенств

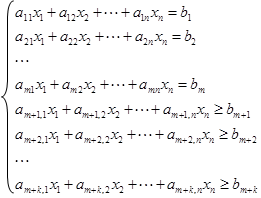(7.80)

и линейная функция