Реферат: Компьютерное математическое моделирование в экономике
Таким образом, данное базисное решение является оптимальным, и minf = -1 при x1 = О, х2 = 0, хз = 1, x4 = 3.
Приведем алгоритм симплекс-метода в общем виде. Обычно все вычисления по симплекс-методу сводят в стандартные таблицы.
Запишем систему ограничений в виде
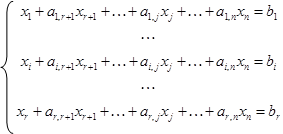 |
(7.90)
а функцию f
![]() (7.91)
(7.91)
Тогда очередной шаг симплекс-процесса будет состоять в переходе от старого базиса к новому таким образом, чтобы значение линейной функции, по крайней мере, не увеличивалось.
Данные о коэффициентах уравнений и линейной функции занесем в табл. 7.12.
Таблица 7.12
Симплекс-таблица
| Базис | Св.чл. | … | … | … | … | ||||||
| 1 | … | 0 | … | 0 | … | … | |||||
| … | … | … | … | … | … | … | … | … | … | … | … |
| 0 | … | 1 | … | 0 | … | … | |||||
| … | … | … | … | … | … | … | … | … | … | … | … |
| 0 | … | 0 | … | 1 | … | … | |||||
| 0 | … | 0 | … | 0 | … | … |
Сформулируем алгоритм симплекс-метода применительно к данным, внесенным в табл. 7.12.
1. Выяснить, имеются ли в последней строке таблицы положительные числа (γ0 не принимается во внимание). Если все числа отрицательны, то процесс закончен; базисное решение (b1 , b2 , ..., br , 0, ..., 0) является оптимальным; соответствующее значение целевой функции f = γ0 . Если в последней строке имеются положительные числа, перейти к п. 2.
2. Просмотреть столбец, соответствующий положительному числу из последней строки, и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов положительных чисел нет, то оптимального решения не существует. Если найден столбец, содержащий хотя бы один положительный элемент (если таких столбцов несколько, взять любой из них), пометить этот столбец и перейти к п. 3.
3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку таблицы, соответствующую наименьшему частному. Выделить разрешающий элемент, стоящий на пересечении отмеченных строки и столбца. Перейти к п. 4.
4. Разделить элементы выделенной строки исходной таблицы на разрешающий элемент (на месте разрешающего элемента появится единица). Полученная таким образом новая строка пишется на месте прежней в новой таблице. Перейти к п. 5.
5. Каждая следующая строка новой таблицы образуется сложением соответствующей строки исходной таблицы и строки, записанной в п. 4, которая предварительно умножается на такое число, чтобы в клетках выделенного столбца при сложении появились нули. На этом процесс заполнения новой таблицы заканчивается, и происходит переход к п. 1.
Таким образом, используя алгоритм симплекс-метода применительно к симплекс-таблице, мы можем найти оптимальное решение или показать, что его не существует. Результативность комплекс-метода гарантируется следующей теоремой (приведем ее без доказательства): если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем начинать можно с любого исходного базиса.
Ранее мы предполагали, что если система ограничений задана в виде (7.85), то перед первым шагом она уже приведена к виду(7.86), где bi ≥0 (I=1,2, …, r). Последнее условие необходимо для использования симплекс-метода. Рассмотрим вопрос об отыскании начального базиса.
Один из методов его получения – метод симплексного преобразования.
Прежде всего проверяем, есть ли среди свободных членов отрицательные. Если свободные члены не являются числами неотрицательными, то добиться их неотрицательности можно несколькими способами:
1) умножить уравнения, содержащие отрицательные свободные члены, на –1;
2) найти среди уравнений, содержащих отрицательные свободные члены, уравнение с максимальным по абсолютной величине отрицательным свободным членом и затем сложить это уравнение со всеми остальными, содержащими отрицательные свободные члены, предварительно умножив его на –1.
Затем, используя действия, аналогичные указанным в пп. 3-5 алгоритма симплекс-метода, совершаем преобразования исходной таблицы до тех пор, пока не получим неотрицательное базисное решение.
Пример 2. Найти исходное неотрицательное базисное решение системы ограничений.
 |
Так как условие неотрицательности свободных членов соблюдается, приступим к преобразованиям исходной системы, записывая результаты в таблицу. Согласно алгоритму просматриваем первый столбец. В этом столбце имеется единственный положительный элемент а31 . Делим на 8,654 все коэффициенты и свободный член третьей строки, после чего умножаем каждый коэффициент на 8,704 и складываем с соответствующими коэффициентами второй строки. Первая строка преобразований не требует, так как коэффициент при неизвестном x1 равен нулю. В результате получаем
0,00000 -5,87100 6,54300 -9,99600 7,61800 0,86400
0,00000 0,68512 17,46384 8,57990 -3,19062 9,79929
1,00000 -0,77756 0,97677 0,89808 0,62769 1,11584
Продолжая просматривать второй столбец и совершая аналогичные преобразования, имеем
0,00000 0,00000 156,19554 63,52761 -19,72328 84,83688
0,00000 1,00000 25,49013 12,52318 -4,65701 14,30299
1,00000 0,00000 20,79687 10,63560 -2,99341 12,24727