Реферат: Компьютерное математическое моделирование в экономике

Требуется найти такое неотрицательное решение

(7.82)

системы (7.80), чтобы функция/принимала наименьшее (или наибольшее) значение.

Условия (7.80) называют ограничениями данной задачи, а функцию f - целевой функцией (или линейной формой). В приведенных выше примерах ограничения имели вид не уравнений, а неравенств. Заметим, что ограничения в виде неравенств, всегда можно свести к системе в виде равенств (способом введения добавочных неизвестных).

Так, для неравенства

(7.83)

вводя добавочное неизвестное х_n+1 , получаем

(7.84)

Потребовав его неотрицательности наряду с остальными неизвестными, получим, что условие х_n+1 ³ 0 превращает (7.84) в (7.83). Введя по отдельному дополнитель­ному неизвестному для каждого из неравенств, получим систему уравнений, равно­сильную исходной системе неравенств.

Пример . Дана система неравенств

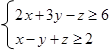Сведем ее к системе уравнений. Получим

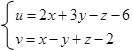После оптимизации значениями дополнительных неизвестных следует пренебречь.

СИМПЛЕКС-МЕТОД

Для решения ряда задач линейного программирования существуют специальные методы. Есть, однако, общий метод решения всех таких задач. Он носит название симплекс-метода и состоит из алгоритма отыскания какого-нибудь произвольного допустимого решения и алгоритма последовательного перехода от этого решения к новому допустимому решению, для которого функция f изменяется в нужном направлении (для получения оптимального решения).

Пусть система ограничений состоит лишь из уравнений

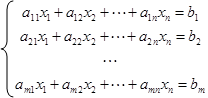(7.85)

и требуется отыскать минимум линейной функции (7.81). Для отыскания произ­вольного опорного решения приведем (7.85) к виду, в котором некоторые r неиз­вестных выражены через остальные, а свободные члены неотрицательны (как это сделать - обсудим позднее):

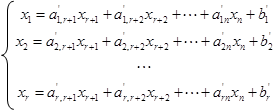
(7.86)

Неизвестные х₁ , х₂ , ..., х_r - базисные неизвестные, набор {х₁ , х₂ , ..., х_r } называется базисом, а остальные неизвестные {x_{r +1} , х_r+2 , …, х_n } - свободные. Подставляя (7.86) в (7.81), выразим функцию f через свободные неизвестные:

(7.87)

Положим все свободные неизвестные равными нулю:

(7.88)

Найдем из системы (7.86) значения базисных неизвестных

(7.89)

Полученное таким образом допустимое решение

отвечает базису x₁ , x₂ , ..., х_r , т.е. является базисным решением. Допустим для определенности, что мы ищем минимум f . Теперь нужно отданного базиса перейти к другому с таким расчетом, чтобы значение линейной функции f при этом умень­шилось. Проследим идею симплекс-метода на примере.

Пример 1 . Дана система ограничений

Требуется минимизировать линейную функцию f = х₂ – х₃ . В качестве свободных переменных выберем х₂ и x₃ . Тогда данная система ограничений преобразуется к виду

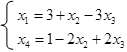Таким образом, базисное решение (3, О, О, 1). Так как линейная функция уже запи­сана в свободных неизвестных, то ее значение для данного базисного решения f = 0. Для уменьшения этого значения можно уменьшить х₂ или увеличить х₃ . Но х₂ в данном базисе равно нулю и потому его уменьшать нельзя. Попробуем увеличить x₃ . Первое из уравнений имеет ограничение х₃ = 1 (из условия х₁ ³ 0), второе - не дает ограничений. Далее, берем х₃ = 1, х₂ не меняем и получаем новое допустимое решение (О, О, 1, 3), для которого f = -1 - уменьшилось. Найдем базис, которому соответствует это решение (он состоит, очевидно, из переменных x₃ , х₄ ). От преды­дущей системы ограничений переходим к новой:

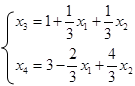а форма в новых свободных переменных имеет вид

Теперь попробуем повторить предыдущую процедуру. Для уменьшения f надо уменьшить либо x_1, либо х₂ , но это невозможно, так как в этом базисе