Реферат: Корректирующие цепи и линии задержки

1. Назначение линий задержки и их основные характеристики

При решении многих задач техники связи и родственных ей областей возникает необходимость в построении электрической цепи, которая запоминала бы аналоговый сигнал, а затем повторяла бы его на выходе цепи через заданное время. Такие цепи называют линиями задержки (ЛЗ).

По конструктивному исполнению ЛЗ подразделяют на электрические, электромеханические, пьезоэлектрические, ультразвуковые, акустические, цифровые и т.д. Электрические ЛЗ являются наиболее распространенным типом, поэтому они и рассматриваются в дальнейшем.

Независимо от принципа работы ЛЗ представляет собой четырехполюсник, на выходе которого сигнал появляется спустя некоторое время после подведения его ко входу

,

где - выходной сигнал,

- входной сигнал,

- время задержки.

- коэффициент пропорциональности.

ЛЗ может выполняться в виде единого блока, либо в виде системы с отводами.

Вполне очевидно, что в идеальной ЛЗ должны выполняться условия безыскаженной передачи сигналов, т.е.

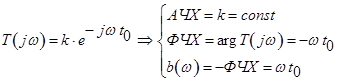
При этом время задержки

На рисунке 1 показаны графики некоторого входного и задержанного неискаженного выходного сигналов при .

Рисунок 1

Передаточная функция идеальной ЛЗ не может быть реализована электрической цепью с конечным числом элементов R , L и С (характеристиками идеальной ЛЗ обладает длинная линия без потерь, что и используется в технике СВЧ).

Описание реальной ЛЗ обычно осуществляется в рамках следующих основных характеристик и показателей:

а) Характеристика группового времени задержки и величина отклонения характеристики группового времени задержки от идеальной (рисунок 2).

В ряде случаев вместо требований к характеристике задают требования к ФЧХ или к характеристике рабочей фазы (см. рисунок 3).

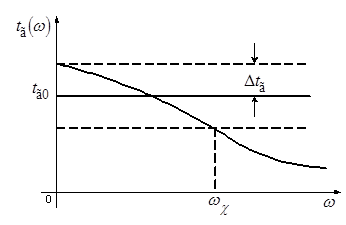
Рисунок 2

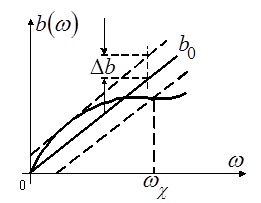
Рисунок 3

б) АЧХ линии задержки и величина ее отклонения от идеальной.

Из условий безыскаженной передачи сигналов следует, что АЧХ ЛЗ должна быть постоянной величиной в рабочей полосе частот или отклоняться от этого значения на величину не превышающей некоторой заданной константы (рис. 4).

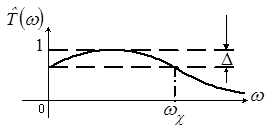
Рисунок 4

--> ЧИТАТЬ ПОЛНОСТЬЮ <--