Реферат: Коррекция дискретных систем управления
- прямое (непосредственное) программирование;
- последовательное (итеративное) программирование;
- параллельное программирование.
Выбор метода зависит от объема памяти, необходимого для размещения постоянных коэффициентов (констант), исходных данных и команд, а также времени и точности вычислений (ошибок накопленных при округлении).
Метод непосредственного программирования
Необходимо реализовать передаточную функцию корректирующего устройства.
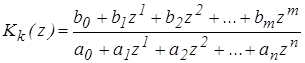 (8)
(8)
При этом система должна быть устойчивой и физически реализуемой (т.е. должно выполняться условие m £ n. )
Разделим полином числителя и знаменателя на zn (или умножим на z-n ).
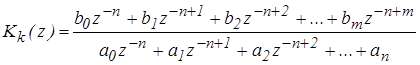 (9)
(9)
Запишем уравнение корректирующего звена в форме z – преобразования
![]()
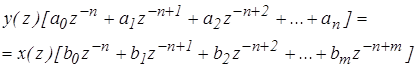 (10)
(10)
![]()
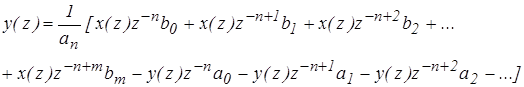 (11)
(11)
Умножение на z-1 соответствует задержке на один такт, а на z-n на n –тактов. Запишем дискретное уравнение корректирующего звена
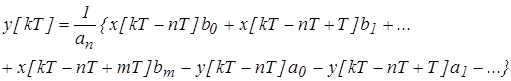 (12)
(12)
Алгоритм позволяет определить значение выходной величины в любой момент времени. Для этого необходимо знать текущее значение входной решетчатой функции и предыдущее значение выходной функции.
Пусть m < n , например m = n-1, при этом x[kT-nT+mT]bm = x[kT-T]bm т.е. необходимо знать предыдущее значение.
Пусть m = n , при этом x[kT-nT+mT]bm = x[kT]bm т. е. необходимо знать текущее значение.
Пусть m > n , например m = n+1, при этом x[kT-nT+mT]bm = x[kT+T]bm т.е. необходимо знать будущее значение (это физически нереализуемо).
Метод параллельного программирования
Разложим дискретную передаточную функцию на простые дроби:
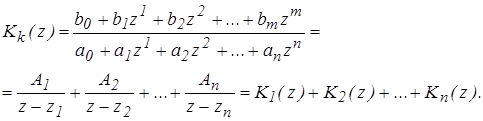 (13)
(13)
Коэффициенты Ai находим методом неопределенных коэффициентов по теореме разложения.
При этом для первого звена можно записать следующие соотношения
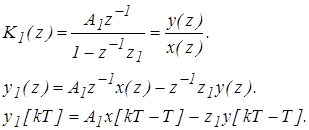 (14)
(14)
Аналогичные соотношения можно записать для любого выхода. При этом передаточная функция может быть представлена в виде схемы, представленной на рис.
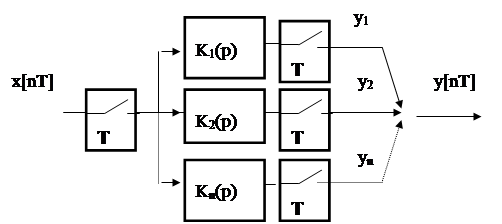 |
Å
|
Достоинство метода : высокое быстродействие.
Недостаток : необходимо много оборудования, меньше надежность.
Метод последовательного программирования
Передаточную функцию можно представить в виде: