Реферат: Краевые задачи и разностные схемы

– вектор искомых коэффициентов,

– соответственно прямая и обратная верхне-треугольные матрицы коэффициентов. Первая из них выглядит так:

.

Обратная матрица удобна при использовании математических пакетов для решения векторно-матричного уравнения. Если , то коэффициенты легко вычисляются последовательной подстановкой значений , начиная с .

Начальные условия для вычисляются по выражениям для следующим образом:

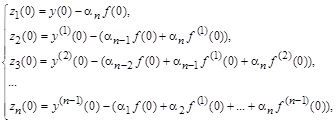
или в векторно-матричной форме:

,

.

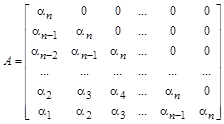2. Разностное представление систем дифференциальных уравнений

Представление системы дифференциальных уравнений первого порядка с начальными условиями

можно заменить системой конечно-разностных уравнений первого порядка с целочисленной независимой переменной i ():

,

погрешность аппроксимации которого пропорциональна сеточному шагу h .

Выше было уже показано, как можно уменьшить погрешность аппроксимации, делая ее пропорциональной . В частности это можно сделать, использовав среднее арифметическое двух разностей первого порядка: “вперед” и “ назад”.

При такой замене производной мы получаем систему разностных уравнений, состоящую из разностных уравнений второго порядка, требующих, кроме известного вектора начальных условий , еще один дополнительный вектор :

.

Дополнительный вектор начальных условий достаточно вычислить по формуле Эйлера. Он и определит дополнительное начальное условие с ошибкой, пропорциональной второй степени h :

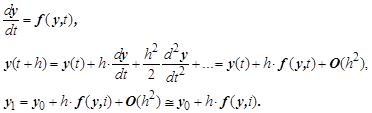
Подстановка таких начальных условий в решение сохранит погрешность результатов на уровне . В таком случае говорят, что разностная схема имеет второй порядок точности.

3. Разностные системы уравнений для краевых задач

Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности - на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей.

Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной.

Для линейной системы уравнений первого порядка, записанной в матричной форме относительно вектора как

,

обязательно задается полный набор краевых условий , включающий хотя бы одно значение , или набор комбинаций из значений и