Реферат: Краевые задачи и разностные схемы
При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями.
Преобразование их в конечно-разностную систему алгебраических уравнений осуществляется аналогично: для каждой точки в области (интервале) интегрирования, где не задано краевое или граничное значение искомой функции, записывается исходное уравнение, в котором все производные выражены через заранее определенное число близлежащих ординат искомой функции, принадлежащих области, и вычислены все коэффициенты и функции независимых переменных в этой точке. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области. В результате будет сформирована алгебраическая система уравнений с числом уравнений и неизвестных, равном общему числу точек области интегрирования.
В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Это достигается многократным применением оператора сдвига к соответствующему конечно-разностному оператору.
Если в центральных точках точность аппроксимации производных с n точками удовлетворяет поставленным требованиям и эту точность желательно сохранить и в приграничных точках заданных областей, то для последних выбирают аппроксимирующие формулы, построенные для (n +1)- й точки или более.
Рассмотрим примеры аппроксимации дифференциальных уравнений с краевыми условиями конечно-разностной системой алгебраических уравнений. Эти аппроксимации в литературе получили название "разностные схемы". Ниже в четырех таблицах приведены четыре варианта конечно-разностной аппроксимации одной и той же краевой задачи, для которой известно точное решение. Вид уравнения, условия на границе интервала, решение аналитическое и вычисленное в заданных точках с 12 значащими цифрами приведены в правой крайней колонке первой таблицы. В левых колонках первой и в трех остальных таблицах записаны системы алгебраических уравнений, полученных применением трех-, пяти-, пяти-шести- и семи точечной аппроксимации второй производной в заданном уравнении. Справа от уравнений приведены решения алгебраических уравнений тоже с 12-ю значащими цифрами.
| Система уравнений с трехточечным представлением производных | Вектор разностного решения с шагом h =0.1 |  |
-199 +100 +0.1=0 | 0.0186590989712 | 0.0186415437361 |
100-199+100 +0.2=0 | 0.0361316064473 | 0.0360976603850 |
100-199+100 +0.3=0 | 0.0512427953890 | 0.0511947672548 |
100-199+100 +0.4=0 | 0.0628415300546 | 0.0627828520998 |
100-199+100 +0.5=0 | 0.0698118753674 | 0.0697469636621 |
100-199+100 +0.6=0 | 0.0710840847137 | 0.0710183518969 |
100-199+100 +0.7=0 | 0.0656455142231 | 0.0655851465687 |
100-199+100 +0.8=0 | 0.0525504484304 | 0.0525024675253 |
| 100-199+0.9=0 | 0.0309298757856 | 0.0309018656257 |
Система уравнений для пяти-точечного представления производных | Вектор решения |
| -9940+3000+2000-500+6=0 | 0.0186406186406 |
| 8000-14940+8000-500+12=0 | 0.0360968696594 |
| -500+8000-14940+8000-500+18=0 | 0.0511941848390 |
| -500+8000-14940+8000-500+24=0 | 0.0627825213460 |
| -500+8000-14940+8000-500+30=0 | 0.0697468774179 |
-500+8000-14940+8000-500 8+36=0 | 0.0710184988305 |
| -500+8000-14940+8000-500+42=0 | 0.0655854996422 |
| -500+8000-14940+8000+48=0 | 0.0525029672554 |
| -500+2000+3000-9940+54=0 | 0.0309024932693 |
| Система уравнений для пяти- и шести точечного представления производных | Вектор решения |
| -3720-1000+3500-1500+250+3=0 | 0.0186415486274 |
| 8000-14940+8000-500+12=0 | 0.0360976918947 |
| -500+8000-14940+8000-500+18=0 | 0.0511948294923 |
| -500+8000-14940+8000-500+24=0 | 0.0627829167486 |
| -500+8000-14940+8000-500+30=0 | 0.0697469746974 |
| -500+8000-14940+8000-500+36=0 | 0.0710183243686 |
| -500+8000-14940+8000-500+42=0 | 0.0655851063829 |
| -500+8000-14940+8000+48=0 | 0.0525024168959 |
| 250-1500+3500-1000-3720+27=0 | 0.0309018105849 |
| Система уравнений для семиточечного представления производных | Вектор решения |
| -7260-12750+23500-14250+4650-650+9=0 | 0.0186415513486 |
| 11400-20910+10000+750-600+100+18=0 | 0.0360976659970 |
| -1350+13500-24410+13500-1350+100+27=0 | 0.0511947713313 |
| 10-135+1350-2441+1350-135+10+3.6=0 | 0.0627828547351 |
| 10-135+1350-2441+1350-135+10+4.5=0 | 0.0697469648318 |
| 10-135+1350-2441+1350-135+10+5.4=0 | 0.0710183515790 |
| 100-1350+13500-24410+13500-1350+63=0 | 0.0655851447467 |
| 100-600+750+10000-20910+11400+72=0 | 0.0525024640963 |
| -650+4650-14250+23500-12750-7260+81=0 | 0.0309018602217 |
В этой задаче весь интервал интегрирования [0,1] был разбит на 10 равных частей с шагом h =0.1. Из одиннадцати точек в двух крайних искомая функция x (t ) была задана, поэтому уравнения записывались для девяти внутренних точек, в которых значения функции требовалось найти.
5. Разностные схемы для уравнений в частных производных
Конечно-разностная аппроксимация дифференциальных уравнений в частных производных, называемая в литературе методом сеток , использует те же конечно-разностные выражения производных через значения искомой функции, которые приведены в таблицах выше. Однако есть особенности, которые связаны с наличием у каждой рассматриваемой точки соседних точек не только по направлениям осей независимых переменных, но и во множестве других наклонных направлений.
Поэтому, в случае использования многоточечных (более трех точек) формул для производных, выражения последних могут разрабатываться дополнительно для каждого применения.
Наиболее удобным в разработке многоточечных конечно-разностных выражений для уравнений в частных производных является операторный метод, основанный на учете взаимосвязи оператора дифференцирования с операторами сдвига по направлениям различных независимых переменных. Рассмотрим его применение на примере построения разностных формул для двумерных уравнений в частных производных второго порядка.
Характерным представителем уравнений в частных производных второго порядка является уравнение Лапласа:
,
где 
– непрерывная функция, заданная на границе области.
Область численного решения уравнения разобьем на клетки системой вертикальных и горизонтальных прямых, проходящих через равномерно расположенные с шагом h точки на осях координат соответственно x и y :
Значения функции в узлах сетки обозначим через 
и для каждой точки области решений частные производные из уравнения заменим соответствующим (например, трех точечным) симметричным конечно-разностным выражением для внутренних точек и для точек вблизи границ таким несимметричным, чтобы значения функций не выходили за пределы области:
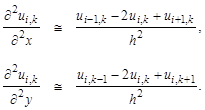
После подстановки в уравнение Лапласа этих выражений для каждой внутренней точки области будет получена система алгебраических уравнений следующего вида:
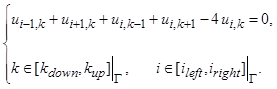
В качестве примера, демонстрирующего применение метода сеток, приведем решение уравнения Лапласа для прямоугольной области с количеством узлов 
и значениями функции на границе, как показано ниже:
| u(0,0) | 0.5 | 0.476 | 0.404 | 0.294 | 0.154 | 0 |
| 0.5 | u(1,1) | u(1,2) | u(1,3) | u(1,4) | u(1,5) | 0 |
| 0.476 | u(2,1) | u(2,2) | u(2,3) | u(2,4) | u(2,5) | 0 |
| 0.404 | u(3,1) | u(3,2) | u(3,3) | u(3,4) | u(3,5) | 0 |
| 0.294 | u(4,1) | u(4,2) | u(4,3) | u(4,4) | u(4,5) | 0 |
| 0.154 | u(5,1) | u(5,2) | u(5,3) | u(5,4) | u(5,5) | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Уравнения для 25 внутренних точек u (i,k ):
|
0.5-4·u(1,1)+u(1,2)+u(2,1) +0.5=0, u(1,1)-4·u(2,1)+u(2,2)+u(3,1)+0.476=0, u(2,1)-4·u(3,1)+u(3,2)+u(4,1)+0.404=0, u(3,1)-4·u(4,1)+u(4,2)+u(5,1)+0.294=0, u(4,1)-4·u(5,1)+u(5,2)+0.154=0, 0.476+u(1,1)-4·u(1,2)+u(1,3)+u(2,2)=0, К-во Просмотров: 297
Бесплатно скачать Реферат: Краевые задачи и разностные схемы
|