Реферат: Квантовая статистика

.

.

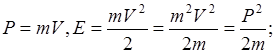
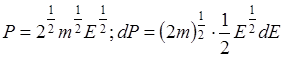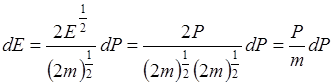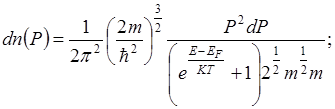
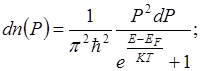
При T=0, f(E,0) =1.

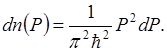
Работа выхода электрона из металла. Термоэлектронная эмиссия.

Формулы Ричардсона и Ричардсона-Дэшмана

Высокая электропроводимость металлов говорит о том, что электроны способны сравнительно свободно перемещаться внутри всей кристаллической решетки металла.

Затруднен их выход из металла, в вакуум, требующей затраты некоторой энергии, называемой 'работой выхода'.

Это навело на мысль рассматривать металл в первом приближении, просто как потенциальную яму, внутри которой (т.е. в металле) потенциальная энергия электрона равна нулю U0=0, а вне металла, т.е. в вакууме U>0. Эта упрощенная модель позволила объяснить многие явления.

Работа выхода - энергия, которую нужно затрачивать, чтобы энергия электрона стала больше высоты потенциального барьера в поверхностном слое металла. И благодаря туннельному эффекту электрон может покинуть металл.

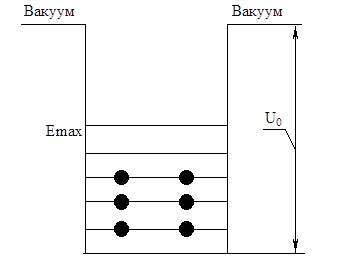
По принципу Паули на каждом энергетическом уровне может находится max два электрона с противоположными спинами (два квантовых состояния).

верхняя граница заполненных уровней при T=0 (уровень Ферми).

- максимальный импульс при Т=0.

Для серебра

- плотность серебра.

A=107,9 - атомный вес (а. е. м).

или

Работа выхода

Глубина потенциальной ямы , с квантовой точки зрения работа выхода равна разности высоты потенциального барьера и энергии Ферми

Работа выхода характеризует минимальную энергию, которую надо сообщить свободному электрону, находящемуся на уровне Ферми, чтобы он мог преодолеть потенциальный барьер на поверхности твердого тела и выйти за пределы металла,

При комнатной температуре число электронов, энергия которых достаточна для преодоления этого барьера, очень невелика. Однако их число резко возрастает с повышением температуры.

Явление испускания электронов нагретыми телами, называется термоэлектронной эмиссией.

Расчет плотности тока термоэлектронной эмиссии при некоторой температуре Т для металла с работой выхода А. определяется формулой Ричардсона - Дэшмана:

, где