Реферат: Квантовая теория атома

Вылетающие с термокатода К и ускоренные сетками С₁ и С₂ электроны испытывали столкновения с атомами паров ртути (давление в запаянной трубке составляло ~ 1 мм рт. ст.). Это были как упругие соударения, при которых изменялось только направление движения электронов, а энергия оставалась неизменной, так и неупругие соударения, при которых часть энергии электронов передавалась атомам ртути. При этом согласно I–ому постулату Бора, атом ртути может принять не любое количество энергии, а только определенную энергию для перехода из одного стационарного состояния в другое. Ближайшее к основному невозбужденному состояние отстоит от него на 4,86 эВ. Действительно, при Е_е < 4,86 эВ наблюдались только упругие соударения, при которых электроны не теряли свою энергию, и электронный ток на аноде I_A увеличивался в ростом потенциала на второй сетке С₂ . Когда энергия, накапливаемая электронами в пространстве между катодом и сетками, достигала значения Е_е = 4,86 эВ начинались неупругие соударения. Энергия электронов уменьшалась, ее оказывалось уже недостаточно для преодоления потенциала задержки φ_задерж между сеткой С₂ и анодом А, и ток I_A резко уменьшался. Аналогичный спад тока I_A наблюдался и при φ₂ = 2·4,86; 3·4,86 … и т.д., когда электроны испытывали 2, 3 … неупругих соударения с атомами ртути.

Эксперименты Франка – Герца подтвердили и второй постулат Бора. Атомы ртути, перешедшие из-за столкновений с электронами в возбужденные состояния, испускали УФ излучение, что соответствовало длине волны λ = с/ν = с·h/(Е₂ – Е₁ ) = 255 нм.

Недостатки теории Бора:

1. Внутренняя противоречивость, непоследовательность (соединение классической физики и квантово-механических постулатов).

2. Никак не объяснялось различие интенсивностей спектральных линий излучения, т.е. не было объяснения тому, что некоторые энергетические переходы оказываются более вероятными, чем другие.

3. Не позволяла создать теоретические модели более сложных атомных систем, например, гелия всего с двумя электронами в атоме.

Теория Бора была заменена последовательной квантовой теорией, учитывающей волновые свойства микрочастиц, получившей название квантовая (волновая) механика.

Стационарное уравнение Шредингера для атома водорода.

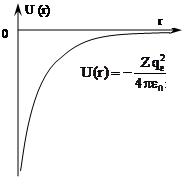
Рассмотрим систему, состоящую из неподвижного ядра с положительным зарядом Z·q_e и одного электрона, вращающегося вокруг ядра. Потенциальная энергия взаимодействия между ними 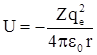. Силовое поле, в котором движется электрон, является центрально–симметричным (потенциальная ловушка гиперболического вида), поэтому целесообразно использовать сферическую систему координат, где r – радиус-вектор, θ – полярный угол, φ – азимутальный угол. Переход от декартовой системы координат к сферической осуществляется по следующим формулам: .

Легко проверить, что тогда выполняется соотношение .

Оператор Лапласа 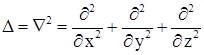в сферических координатах имеет вид

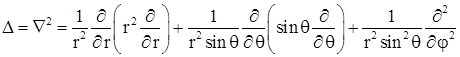
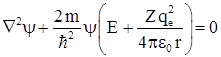Стационарное уравнение Шредингера для рассматриваемой задачи можно записать как , или в сферических координатах

Для решения дифференциальных уравнений такого типа используется метод разделения переменных, поэтому решение ищется в виде или, совмещая функции угловых координат . При дифференцировании по r функция считается постоянной, при дифференцировании по угловым координатам θ и φ функция R(r) – также постоянной.

После подстановки в уравнение получаем

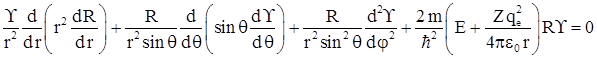
Умножим обе части уравнения на и проведем разделение переменных, тогда

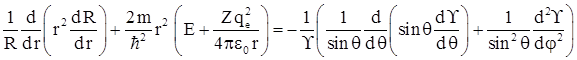
В левую часть уравнения входят величины, зависящие только от r, а в правой части – величины, зависящие только от угловых координат θ и φ. Такое возможно только в том случае, если обе части уравнения равны некоторой постоянной величине, которую называют постоянной разделения. Пусть эта постоянная разделения равна l (l +1), где l – целые числа. Итак, для левой части уравнения получаем 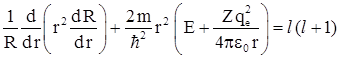или

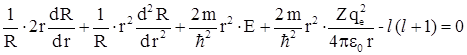
После умножения уравнения на получаем:

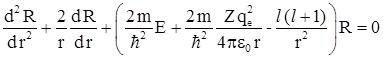
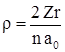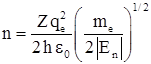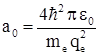Введем безразмерную переменную и безразмерный энергетический параметр . Здесь – боровский радиус , а nсовпадает с величиной n, выраженной из ранее полученного выражения для энергии электрона в n – ном стационарном состоянии.

Тогда решение последнего уравнения для R(r) получается в виде , где – присоединенные полиномы Лагерра порядка р и степени m, причем . Таким образом, функция R(r) оказывается функцией двух целых чисел nи l.

Угловая часть волновой функции также ищется с помощью разделения переменных (θ и φ) и имеет вид , где – полиномы Лежандра от аргумента , а число m принимает следующие значения . Функция угловых координат определяется целыми числами lи m.

Полная координатная часть волновой функции, являющейся решением уравнения Шредингера, имеет вид .

Для основного невозбужденного состояния (при n = 1, l = 0, m = 0) угловая часть , и волновая функция записывается в виде .

Постоянная С определяется из условия нормировки вероятности на единицу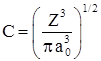.