Реферат: Квантовая теория атома

Определим для этого случая постоянную С. Условие нормировки вероятности на единицу имеет вид 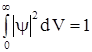. Подставляя выражение для с учетом того, что , получаем .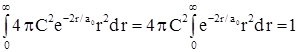

Воспользовавшись соотношением 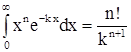(для нашего случая 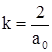и ), получаем 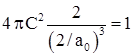или и окончательно .

Тогда нормированная волновая функция .

Собственные значения уравнения Шредингера, определяющие энергию электрона в атоме, совпадают с полученными ранее по теории Бора:

или где n = 1, 2, 3 …

Таким образом, энергетические уровни стационарных состояний электрона определяются только главным квантовым числом n.

Каждому значению n соответствует l = 0, 1 ,2 …(n – 1), всего nзначений,

каждому значению lсоответствует m = 0, ±1, ±2, …. ± l, всего (2l + 1) значений. Следовательно, каждому значению nсоответствует возможных ψ – функций, т.е. кратность вырождения энергетических уровней равна n² .

C9-4

Значение квантовых чисел как следствие стационарного уравнения Шредингера:

n– главное квантовое число, определяющее энергетические уровни электрона в атоме,

n = 1, 2, 3 …

l– орбитальное (азимутальное) квантовое число, определяющее момент импульса электрона в атоме (механический орбитальный момент), l = 0, 1, 2, … (n – 1).

Одним из важнейших следствий уравнения Шредингера является квантование орбитального момента импульса электрона: ,

т.е. модуль орбитального момента может принимать лишь значения, кратные ћ и определяемые орбитальным квантовым числом l.

m– магнитное квантовое число, задающее проекцию момента импульса электрона на направление внешнего магнитного поля, m= 0, ±1, ±2, … ± l.

В квантовой механике существует строгое доказательство того, что вектор момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_lz на направление внешнего магнитного поля (OZ) принимает квантованные значения, кратные ћ и определяемые магнитным квантовым числом m:L_lz = ћ·m.

Это следствие решения уравнения Шредингера для водородоподобных систем называется пространственным квантованием.

Как уже говорилось, понятие орбиты электрона в квантовой механике носит вероятностный характер. Вероятность обнаружения электрона в единичном объеме отличается в различных точках пространства и может

быть определена через волновую

функцию

По теории Бора вероятность dw ≠ 0 только для r = a₀ (для n= 1). При квантово-механическом рассмотрении существует ненулевая вероятность обнаружения электрона в любой точке пространства, но эта вероятность имеет максимальное значение в окрестности r = a₀ : электрон как бы «размазан» в пространстве, образуя электронное облако, густота (плотность) которого характеризует вероятность нахождения в данной точке. При этом квантовые числа nи lопределяют размер и форму электронного облака, а m характеризует ориентацию облака в пространстве.

Описание состояние электронов в атоме. В зависимости от квантовых чисел вводится определенная символика обозначения состояния электрона:

l = 0	S - состояние	Shapp (резкая) серия излучения
l = 1	p - состояние	Principal (главная)
l = 2	d - состояние	Diffuse (диффузная)
l = 3	f - состояние	Fundamental (основная),
и далее по английскому алфавиту (g, h …)

Значение главного квантового числа nуказывается перед орбитальным числом l:

1S (n = 1, l =0, m = 0)

2S (n = 2, l =0, m = 0), 2p (n = 2, l =1, m= ±1)