Реферат: Лабораторная по ЭММ

1. Проверить наличие аномальных наблюдений.

2. Построить линейную модель Ŷ(t)=a₀ +a₁ t, параметры которой оценить МНК (Ŷ(t) – расчетные, смоделированные значения временного ряда).

3. Построить адаптивную модель Брауна Ŷ(t)=a₀ +a₁ k с параметром сглаживания α=0,4 и α=0,7; выбрать лучшее значение параметра сглаживания.

4. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7-3,7).

5. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.

6. По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р =70%).

7. Фактические значения показателя, результаты моделирования и прогнозирования представить графически.

Решение

1. Проверим наличие аномальных наблюдений методом Ирвина:

,

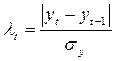где ,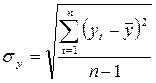

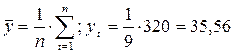
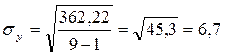
Все , следовательно среди наблюдений нет аномальных.

2. Оценка параметров модели с помощью Excel.

Построим линейную однопараметрическую модель регрессии .

Таблица 5

t	Y
1	45
2	43
3	40
4	36
5	38
6	34
7	31
8	28
9	25

Оформим необходимые данные в Таблицы 6 и 7.

Таблица 6

Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	47,64	0,94	50,49
t	-2,42	0,17	-14,41

Таблица 7

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	45,22	-0,22
2	42,81	0,19
3	40,39	-0,39
4	37,97	-1,97
5	35,56	2,44
6	33,14	0,86
7	30,72	0,28
8	28,31	-0,31
9	25,89	-0,89
сумма	0,00

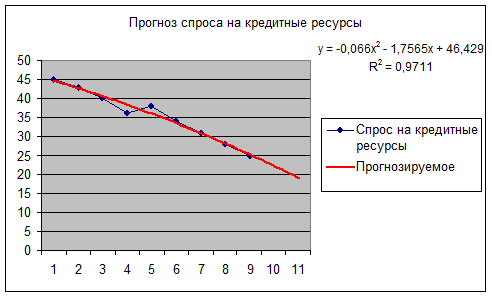
Уравнение регрессии зависимости (спрос на кредитные ресурсы) от (времени) имеет вид:

Коэффициент детерминации равен R ² =0,967. Само значениеR ² показывает, что изменение во времени спроса на кредитные ресурсы на 96,7 % описывается линейной моделью.

Угловой коэффициент а ₁ = -2,42 уравнения показывает, что за одну неделю спрос на кредитные ресурсы банка уменьшается в среднем на 2,42 млн. руб.

При вычислении «вручную» по формуле

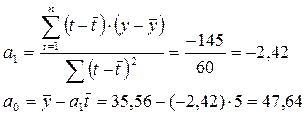
получаем те же результаты.

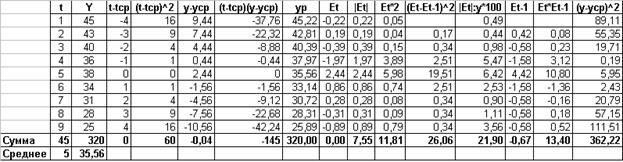
Рис. 2.

Оценка параметров модели Брауна, при α=0,4
t	Y(t)	a0	a1	Yp(t)	E(t)
0	47,64	-2,42
1	45	45,07	-2,45	45,22	-0,22
2	43	42,9	-2,42	42,81	0,19
3	40	40,6	-2,36	40,39	0,39
4	36	39,23	-2,04	37,97	1,97
5	38	34,12	-1,65	35,56	2,44
6	34	33,7	-1,51	33,14	0,86
7	31	30,9	-1,46	30,72	0,28
8	28	28,5	-1,41	28,31	0,31
9	25	26,5	-1,27	25,89	0,89

Оценка параметров модели Брауна, при α=0,7
t	Y(t)	a0	a1	Yp(t)	E(t)
0	47,64	-2,42
1	45	45,1	-2,44	45,22	-0,22
2	43	42,7	-2,43	42,81	0,19
3	40	40,6	-2,39	40,39	0,39
4	36	38,97	-2,21	37,97	1,97
5	38	36,9	-1,99	35,56	2,44
6	34	33,58	-1,91	33,14	0,86
7	31	30,9	-1,88	30,72	0,28
8	28	28,5	-1,85	28,31	0,31
9	25	26,34	-1,77	25,89	0,89

4. Оценим адекватность построенной модели. Рассчитанные по модели

значения прибыли(t =1, 2,…, 9).

Проверим независимость остатков с помощью d-критерия Дарбина-Уотсона:

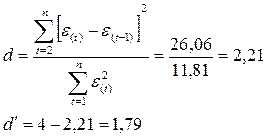
Критические значения d ‑статистики для числа наблюдений n =9 и уровня значимости a=0,05 составляют: d ₁ =0,82; d ₂ =1,32.

Так как выполняется условие

,

то статистическая гипотеза об отсутствии автокорреляции в остатках не отклоняется на уровне значимости a=0,05.

Для достоверности проверим отсутствие автокорреляции в остатках также и по коэффициенту автокорреляции остатков первого порядка, который равен:

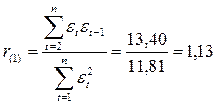
Критическое значение коэффициента автокорреляции для числа наблюдений n =9 и уровня значимости a=0,05 составляет 0,666. Так как коэффициент автокорреляции остатков первого порядка не превышает по абсолютной величине критическое значение, то это еще раз указывает на отсутствие автокорреляции в остатках.