Реферат: Лекции по физике

Лекция 10

8.5. Линии равной толщины

Как ясно уже из заголовка, речь пойдет о пластинах (тонких пленках), толщина которых непостоянна. И, по существу, здесь не решается какая-то новая задача: механизм интерференции тот же, что и в случае плоскопараллельной пластине. Можно, например, зафиксировать величину угла падения q , и мы получим готовую формулу, подставив в соответствующее выражение зависимость d от координат. Обычно принимают значение q =0 - в общем виде выражение громоздко и не представляется полезным.

n=1 q 1 2 0 X d0 n>1 a

Для реальной пластины зависимость d от координат может быть какой угодно. Традиционно рассматриваются лишь некоторые частные случаи такой зависимости.

Например, пластина может иметь форму клина. У показанной на рисунке пластины толщина зависит от координаты x :

; .

Для соседних максимумов, очевидно, D k=1 , и мы имеем для ширины интерференционной полосы:

; .

Мы, вроде, получили новую формулу, но, оказывается, она нам знакома. Действительно, после отражения от поверхностей и преломления лучи 1 и 2 расходятся под углом q =2 a n , мы же при анализе интерференции волн от двух точечных источников получили для ширины интерференционной полосы выражение . Оно оказывается справедливым и в этом случае, но тут появляются некоторые проблемы.

экран изображ. поверхности 1 2 локализации линза 1 2 поверхность локализации пластина

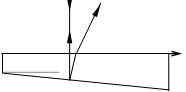
При интерференции волн от двух точечных источников волны реально, “на самом деле” взаимодействуют, складываются на поверхности экрана. Теперь же эти волны (1 и 2 ) после отражения от двух поверхностей расходятся под углом q . Возникает вопрос, где же они интерферируют друг с другом или, как принято выражаться, где локализованы интерференционныу полосы.

Ответ на этот вопрос поясняется рисунком. Для наблюдения интерференции отраженных от поверхностей пластины (клина) волн используется линза и экран, на котором создается изображение поверхности локализации интерференционных полос. Эта последняя образована точками пересечения продолжений луча 1 (он “начинается” от верхней поверхности пластины) и луча 2 после его преломления.

Другая традиционно рассматриваемая задача - кольца Ньютона. Это также линии равной толщины, но роль пластины здесь играет воздушный промежуток между плоской поверхность стеклянной, например, пластины и выпуклой поверхностью плосковыпуклой линзы.

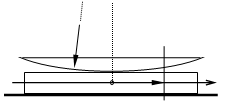
R d(r) r

Пусть угол между вертикалью и прямой, проведенной из центра кривизны к некоторой точке выпуклой поверхности линзы с координатой r , равен a . Тогда

.

Показатель преломления в промежутке между стеклянными поверхностями можно считать равным единице. Поэтому условие максимума будет

; .

При таких значениях радиуса r будут наблюдаться максимумы. Очевидно, минимумы будут при

; .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--