Реферат: Лекции по физике
d
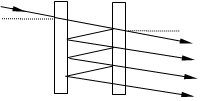
q q
1
2
3
4
На своем пути каждый последующий из пронумерованных лучей испытывает два дополнительных отражения от внутренних поверхностей пластин. Стало быть, их интенсивности различаются в r 2 раз. Интенсивность пропорциональна квадрату амплитуды и поэтому
; 
.
Далее, разность оптических путей соседних лучей равняется 
и разность фаз их колебаний в удаленной точке наблюдения
.
Таким образом, для амплитуды суммарных колебаний мы имеем выражение:
.
Начальную фазу колебаний первого луча мы положили равной нулю.
Для сложения этих колебаний перейдем к комплексным переменным - добавим мнимую часть, памятуя, что физический смысл имеет лишь реальная часть суммы, которую мы получим:
.
Итак, нам надо найти сумму членов бесконечной геометрической прогрессии, знаменатель которой 
. Таким образом,
.
Амплитуда суммарных колебаний равна модулю комплексного значения 
:
.
Воспользовавшись формулой Эйлера, произведем перемножение скобок под квадратным корнем в знаменателе:
.
|
r : E S 0,05 0,25 0,75 0 q |
Вспомним, что
  |
.
Таким образом,
.
Как и ожидалось, с увеличением коэффициента отражения глубина минимумов увеличивается. Одновременно уменьшается ширина интерференционных полос. Предвидеть этот результат было не так просто.
9. Дифракция Фраунгофура
Дифракция рассматривает процессы отклонения направления распространения света от прямолинейного при встрече с некоторыми препятствиями или при отражении от них. В случае дифракции Фраунгофера рассматривается падение на препятствие плоской волны (бесконечно удаленный источник света) и подразумевается, что зона наблюдения удалена от препятствия на достаточно большое расстояние (находится на бесконечности). Коротко говоря, это “дифракция в параллельных лучах”.
Как Вы увидите, основные задачи дифракции Фраунгофера мы, собственно, уже решили. Просто мы говорили о волнах вообще, а словом дифракция обычно обозначают именно оптические явления, поведение в том или ином случае световой (электромагнитной) волны.
9.1. Дифракция на щели
Ранее мы получили такое выражение для углового распределения амплитуды от системы точечных источников, от “цепочки” источников длиной b :
.
Ввиду особой важности да и сложности понимания этого результата получим его еще раз - другим способом.
|
X b К-во Просмотров: 635
Бесплатно скачать Реферат: Лекции по физике
|