Реферат: Лекции по линейной алгебре (МГИЕМ, ФПМ)
Параметр ![]() для поворота плоскости
для поворота плоскости ![]() будем считать изменяющимся mod 2p т. е.
будем считать изменяющимся mod 2p т. е. ![]() =
= ![]() . Такое же соглашение будем использовать и для винтового перемещения
. Такое же соглашение будем использовать и для винтового перемещения ![]() при h > 0. Если же h = 0 , и речь идет о повороте в пространстве, надо учитывать, что
при h > 0. Если же h = 0 , и речь идет о повороте в пространстве, надо учитывать, что ![]() =
= ![]() . В частности,
. В частности, ![]() =
= ![]() (отражение относительно прямой параллельной v и проходящей через О). Аналогично,
(отражение относительно прямой параллельной v и проходящей через О). Аналогично, ![]() =
= ![]() . Если при этом j=p это преобразование не зависит от вектора n и является отражением относительно точки О.
. Если при этом j=p это преобразование не зависит от вектора n и является отражением относительно точки О.
4* Композиции 1.
Теорема 4
Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f·g)* = f*g*(Символом · обозначена композиция перемещений).
Доказательство.
Используем координатную форму записи: f( R) = AR + v, g( R) = BR + w. Тогда: (f·g)( R) = f( (g( R)) = f( BR + w) = A( BR +w) +v = ( AB)R + ( Aw + v). Следовательно, (f·g)* = AB = f*g*.
Следствие.
Композиция двух перемещений с определителями одного знака имеет определитель (+1); если знаки определителей противоположны, композиция имеет определитель (-1).
Вычисление композиции перемещений пространства ![]() не вызывает затруднений. Отметим только, что
не вызывает затруднений. Отметим только, что ![]() ·
·![]() =
= ![]() ,где v =2AB.
,где v =2AB.
Для случая пространства ![]() удобно использовать комплексные числа. Отождествляя их с точками плоскости, получаем удобный способ записи перемещений. Например, поворот
удобно использовать комплексные числа. Отождествляя их с точками плоскости, получаем удобный способ записи перемещений. Например, поворот ![]() можно записать в виде: z ®
можно записать в виде: z ®![]() z + c. Точка О является неподвижной и соответствующее комплексное число
z + c. Точка О является неподвижной и соответствующее комплексное число ![]() находится из уравнения
находится из уравнения ![]() =
= ![]()
![]() + с, откуда
+ с, откуда ![]() = с/(1-
= с/(1-![]() ). Таким образом,
). Таким образом, ![]() Отметим, что
Отметим, что ![]() =
=![]() при j+y№0 (mod 2p) . В то же время при j+y = 0 указанная композиция будет переносом на вектор AD, где D =
при j+y№0 (mod 2p) . В то же время при j+y = 0 указанная композиция будет переносом на вектор AD, где D = ![]() .
.
Преобразование z®![]() +c является скользящим отражением относительно прямой Im(
+c является скользящим отражением относительно прямой Im(![]() = 0 на вектор 0,5 (с +
= 0 на вектор 0,5 (с + ![]() ). Если прямая l проходит через точку
). Если прямая l проходит через точку ![]() и ее направляющий вектор (рассматриваемый как комплексное число) имеет аргумент
и ее направляющий вектор (рассматриваемый как комплексное число) имеет аргумент ![]() , то перемещение
, то перемещение ![]() можно записать в виде
можно записать в виде ![]()
Композиция двух скользящих отражений относительно пересекающихся прямых будет поворотом. В то же время, если прямые параллельны, композиция - перенос.
ГРУППЫ ПРЕОБРАЗОВАНИЙ
(продолжение)
5.Кватернионы
Удобный способ аналитической записи перемещений в пространстве дают кватернионы , являющиеся обобщением комплексных чисел. Чтобы подчеркнуть аналогию между способами построения кватернионов из комплексных чисел и построением комплексных чисел из вещественных сравним обе конструкции.
Построение комплексных чисел Построение кватернионов
|
1. Комплексное число z = a + bi -это матрица |
1. Кватернион q = z + wj - это матрица |
|
Отсюда вытекает, что для этих чисел имеют место те же законы действий, что и для матриц, т.е. ассоциативность умножения и закон дистрибутивности. Непосредственно проверяется коммутативность умножения комплексных чисел(но не кватернионов!) | |
|
2. Число вида a + 0i можно отождествить с вещественным числом a и таким образом |
2. Число вида z + 0j можно отождествить с комплексным числом z и таким образом |
|
|
|
4. Число |
4. Число |
|
Обратное число определено однозначно так как ему отвечает (однозначно определенная !) обратная матрица. | |
|
К-во Просмотров: 248
Бесплатно скачать Реферат: Лекции по линейной алгебре (МГИЕМ, ФПМ)
| |
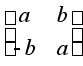 , где
, где 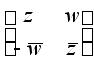 , где
, где