Реферат: Линейное программирование: решение задач графическим способом

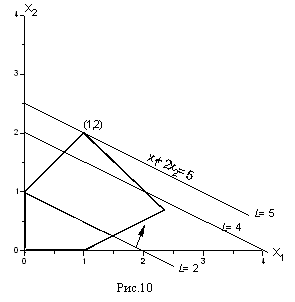
Пусть, например, L =2. Тогда прямая проходит через точки (2,0) и (0,1) и изображена на рис. 8. Будем теперь увеличивать L . Тогда прямая начнёт двигаться параллельно самой себе в направлении, указанном стрелкой. Легко догадаться, что максимальное значение L получится тогда, когда прямая пройдет через вершину многоугольника, указанную на рисунке, и дальнейшее увеличение L приведет к тому, что прямая выйдет за пределы многоугольника и её пересечение с допустимой областью будет пустым.

Выделенная вершина лежит на пересечении прямых

и поэтому имеет координаты . Это и есть решение нашей задачи, т.е. есть оптимальный план задачи (1.41). При этом значение целевой функции , что и дает её максимальное значение.

Обратите внимание на то, что оптимальный план, как правило, соответствует какой-то вершине многоугольника, изображающего допустимую область. И лишь в том случае, когда прямая случиться так, что решение не будет единственным. Но и в этом случае вершины, соответствующие границам этой стороны, дают оптимальные планы нашей задачи линейного программирования. Таким образом, вершины допустимой области играют в решении задач линейного программирования особую роль.

Рис. 9

Ну, а если допустимая область неограничена, то и значение целевой функции может быть неограниченным.

Подводя итог этим примерам, можно сформулировать следующие положения:

1. допустимая область - это выпуклый многоугольник;

2. оптимум достигается в вершине допустимой области (если допустимая область ограничена и не пуста);

3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи.

Гл 2 Решение задач линейного программирования графическим способом на ЭВМ

2.1 Описание работы программы

Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и Graph.

При запуске программы она проверяет возможно ли использование графического интерфейса. Если это возможно то программа переходит к следующему этапу.

Далее процедурой ShowXOY Рисуется на экран координатные оси. На этом работа этой процедуры заканчивается и пользователь в следующей процедуре (EnterNerav и в частности в подпроцедуре GetNerav ) предлагается ввести коэффициенты неравенства a₁ x+a₂ y=b в следующем порядке: a ₁ пробел a ₂ пробел b . Сразу после ввода всех коэффициентов процедурой ShowLine рисуется нужная линия. После нажатия [Esc] процедура EnterNerav заканчивается и передает управление процедуре EnterMainF в которой пользователю предлагается ввести коэффициенты целевой функции. Далее работа переходит к процедуре GetResult где идет подсчет оконцательного товета с помощбю процедуры SolveOprtel где считаетя определитель т. е. точки пересечения целевой функции с каждой линией ограничения. Далее выводится ответ, если это возможно.

Далее следует описание используемых стандартных процедур и функций.

Процедуры и функции модуля System :

Function Frac (X : Real) : Real;

Возвращает дробную часть аргумента.

Параметр X - выражение вещественного типа. Результат - дробная часть X, то есть Frac(X) = X-Int(X) .

Procedure Str (X [: Width [: Decimals ]]; Var S : String);

Преобразовывает число в строку. Преобразовывает числовое значение X в строковое представление этого числа, которое можно выводить операторами типа Write и OutText .

Function Round (X : Real) : Longint;

Округляет значение вещественного типа до значения целочисленного типа. X - выражение с реальным типом. Round возвращает значение типа Longint , которое является значением X, округленного к самому близкому целому числу. Если X – ровно посередине между двумя целыми числами, то результатом будет число с самой большой абсолютной величиной.

Если округленное значение X ненаходится внутри допустимого диапазона Longint , то происходит ошибка во время выполнения программы.

Модуль Crt :

В модуле Crt находятся мощные подпрограммы, которые дают вам возможность полного управления возможностями вашего PC.

Подпрограммы модуля Crt обеспечивают контроль над текстовыми режимами экрана, расширенными кодами клавиатуры, цветами, окнами и звуком.

Crt может использоваться только в программах, предназначенных для IBM PC, AT, PS/2 и полностью совместимых.