Реферат: Линейное программирование, решение задач симплексным методом

Такая идея последовательного улучшения решения и за­ложена в основном вычислительном методе решения задач линейного программирования, получившим название симп­лексного метода.

Симплексный метод на основе полных таблиц

Постановка задачи об определении оптимального ассортимента продукции

Предприятие может производить два вида изделий А и В, располагая для их изготовления ограниченными ресурса­ми материала чугуна и стали соответственно в количествах 350 и 392 кг и оборудования в количестве 408 станко-часов. Данные, представленные в виде таблицы, характеризуют затраты каждого из перечисленных трех видов ресурсов на изготовление одного изделия А и В.

Требуется определить сколько изделий А и В должно про­изводить предприятие, чтобы достичь наибольшей прибыли.

Виды ресурсов	Объем ресурсов	Затраты на одно изделие
		А	В
Чугун	350	14	5
Сталь	392	14	8
Оборудование	408	6	12
Прибыль в руб.	10	5

Введем искомые неизвестные Х₁ и X₂ , обозначающие число изделий А и В, которые должно производить пред­приятие.

Тогда математически задачу можно сформулировать сле­дующим образом.

Среди множества неотрицательных решений системы неравенств

14X₁ + 5Х₂ ≤ 350, (1.1)

14Х₁ + 8Х₂ ≤ 392,

6Х₁ + 12Х₂ ≤ 408,

найти такое решение, для которого функция

Z = 10 Х₁ + 5 Х₂

достигает наибольшего значения.

Геометрическое решение задачи

Прежде всего, построим область допустимых решений, соответствующую системе неравенств.

Для этого, заменив каждое из неравенств равенством

14Х₁ + 5Х₂ = 350, (1-я прямая),

14X₁ + 8Х₂ = 392, (2-я прямая),

6Х₁ + 12Х₂ = 408, (3-я прямая),

строим граничную линию. Учитывая, что Х₁ ≥ 0 и Х₂ ≥ 0, полу­чаем заштрихованную часть плоскости, образующую много­угольник решений OABCD (рис.1).

Затем строим линию уровня 10Х₁ + 5Х₂ = 0 и вектор (10;5), которые взаимно перпендикулярны. Нетрудно показать, что вектор дает направление наибольшего возрастания линей­ной функции.

Действительно

Z₀ = 10X₁₀ + 5Х₂₀ = 10 * 0 + 5 * 0 = 0,

Z_А = 10X_{1 A} + 5Х_{2 A} = 10 * 0 + 5 * 34 = 170,

Z_D = 10X_{1 D} + 5X_{2 D} = 10 * 25 + 5 * 0 = 250 и т. д.

Из всех линий уровня выбираем две, из которых одна проходит через точку 0 и дает min значение функции Z, а другая проходит через точку С и функция Z для нее прини­мает mах значение. Эти линии уровня называются опорными.

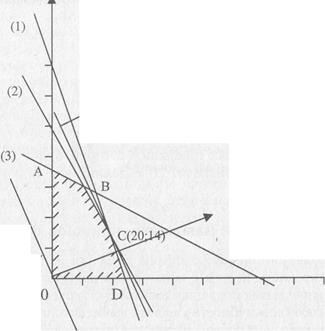
Рис. 1

Точка C образована первой и второй прямыми. Следова­тельно, решая систему уравнений

14Х_l + 5Х₂ = 350,

14Х₁ + 8Х₂ = 392,