Реферат: Линейное программирование
![]()
Тогда получаемый доход
![]() тыс $.
тыс $.
Оптимальному решению всегда соответствует одна из допустимых угловых точек пространства решений. Какая из этих точек окажется оптимальной, зависит от наклона прямой, представляющей целевую функцию (т.е. от коэффициентов целевой функции).
4. Алгебраический метод решения задач
Использование графического метода удобно при решении задач ЛП с двумя переменными. При большем их числе необходимо применение алгебраичского аппарата.
Процесс решения задачи ЛП симплекс-методом носит итерационный характер: однотипные вычислительные процедуры в определённой последовательности выполняются до тех пор, пока не будет получено оптимальное решение.
4.1. Стандартная форма линейных оптимизационных моделей
1. Все ограничения записываются в виде равенств с неотрицательной правой частью. Исходное ограничение можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).
Например,
![]()
Введём остаточную переменную s1>0, тогда
![]()
Правую часть равенства можно сделать неотрицательной, умножив обе части на –1.
2. Значения всех переменных модели неотрицательны.
Любую переменную yi, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:
![]()
При любом допустимом решении только одна из этих переменных может принимать положительное значение, т.к. если ![]() , то
, то ![]() , и наоборот. Это позволяет рассматривать
, и наоборот. Это позволяет рассматривать ![]() как остаточную переменную, а
как остаточную переменную, а ![]() – как избыточную.
– как избыточную.
3. Целевая функция подлежит максимизации или минимизации.
Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот.
Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных в обоих случаях будут одинаковы.
4.2. Симплекс-метод
Общую идею симплекс-метода проиллюстрируем на примере модели для задачи фирмы Reddy Mikks. На исходная точка алгоритма – начало координат (т. A) – начальное решение. От исходной точки осуществляется переход к некоторой смежной угловой точке (т. B или т. F). Её выбор зависит от коэффициентов целевой функции. Т.к. коэффициент при xE больше коэффициента при xI, а целевая функция подлежит максимизации, требуемое направление перехода соответствует увеличению xE (т. B). Далее указанный процесс повторяется для выяснения, существует ли другая экстремальная точка, соответствующая лучшему допустимому решению.
Правила выбора экстремальной точки:
1. Каждая последующая угловая точка должна быть смежной с предыдущей.
2. Обратный переход к предшествующей экстремальной точке не может производиться.
Чтобы описать рассмотренные процедуры формальными способами, необходимо определить пространство решений и угловые точки алгебраически. Требуемые соотношения устанавливаются по таблице:
| Геометрическое определение (графический метод) | Алгебраическое определение (симплекс-метод) |
| Пространство решений | Ограничения модели стандартной формы |
| Угловые точки | Базисные решения задачи в стандартном виде |
4.2.1. Представление пространства решений стандартной задачи ЛП.
Модель:
максимизировать целевую функцию
![]()
при ограничениях
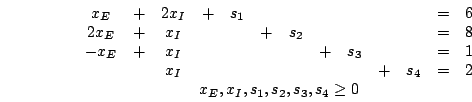
На – пространство решений. Каждую точку можно определить с помощью
![]()
Для идентификации нужной точки воспользуемся тем, что при ![]() ограничения модели эквивалентны равенствам, которые представляются соответствующими рёбрами пространства решений.
ограничения модели эквивалентны равенствам, которые представляются соответствующими рёбрами пространства решений.