Реферат: Линейные метрические, нормированные и унитарные пространства

и

Если положить а = ¥, b = ¥, то квадрат этой нормы в теории сигналов носит название энергии сигнала.

так как такая энергия выделяется на резисторе с сопротивлением в 1 Ом при напряжении x(t) на его зажимах.

Пример. Имеется треугольный импульс длительности t:

Вычислить энергию и норму сигнала.

Решение.

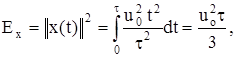
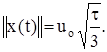
3. Линейное унитарное пространство

Определение. Линейное нормированное пространство R называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов x, yÎR ставит в соответствие действительное или комплексное число (x, y), удовлетворяющее условиям

1. (x, y) = (y, x)* ( _* - знак комплексного сопряжения);

2. (a₁ х₁ + a₂ х₂ , y) = a₁ (x₁ , y) + a₂ (x₂ , y) (a₁ , a₂ ÎK);

3. (x, x) ³ 0, если (х, х) = 0, то х = 0.

В унитарном пространстве норма вводится следующим образом

Теорема 1. Для " х, y унитарного пространства R справедливо неравенство Шварца

Равенство имеет место лишь для линейно зависимых элементов.

Теорема 2. Для " х, y унитарного пространства R имеет место неравенство

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = ly(l > 0).

Теорема 3. Для " х, y унитарного пространства R выполняется равенство параллелограмма

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = ly(l > 0).

Определение. Два элемента х, yÎR (x¹ 0, y¹ 0) называются ортогональными, если (х, y) = 0.

Система элементов e₁ , e₂ , . . . , e_n , . . . унитарного пространства R называется ортонормированной, если