Реферат: Логарифмические частотные характеристики и передаточные функции радиотехнической следящей системы

при ω = K, L(ω) = 0.

Наклон асимптоты будет равен –20 дБ на декаду.

Вторая асимптота строится в диапазоне частот ()

в соответствии с уравнением:

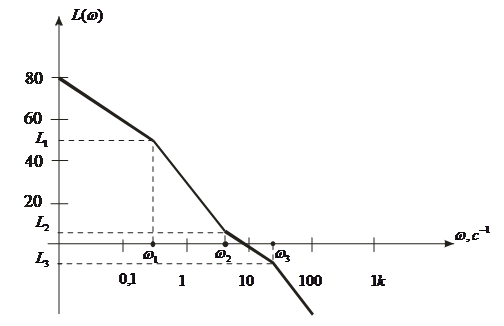
Рис. 1. Логарифмическая амплитудно-частотная характеристика

.

Наклон асимптоты будет равен –40 дБ на декаду.

Третья асимптота строится в диапазоне частот (). Уравнение третьей асимптоты:

Это уравнение прямой, проходящей через точки L (ω₂ ) и L (ω₃ ),

где .

Таким образом, можно записать:

В точке L₂ асимптота изменяет свой наклон на +20 дБ, итоговый наклон третьей асимптоты составляет –20 дБ.

Четвертая асимптота строится в диапазоне частот () в соответствии с уравнением:

Таким образом, при переходе через сопрягающую частоту ω₃ асимптота меняет свой наклон на –20 дБ, и в итоге имеет наклон –40 дБ/дек.

Выводы:

1.При переходе текущего значения частоты через очередную сопрягающую частоту наклон асимптоты изменяется на +20 дБ, если множитель находится в числителе выражения для расчета АЧХ и изменяется на –20 дБ, если этот множитель находиться в знаменателе.

2. Наклон каждой асимптоты кратен 20 дБ /дек.

По ЛАЧХ можно восстановить частотную передаточную функцию.

Передаточные функции следящих систем

Из изложенного выше следует, что любая из передаточных функций: операторный коэффициент передачи W(p), передаточная функция W(s) и частотная передаточная функция (комплексный коэффициент передачи) W(jw) может быть получена путем замены переменных в известном выражении для одной из вышеназванных передаточных функций.

Определим передаточные функции, связывающие входные и выходные переменные в замкнутой следящей системе, представленной математической моделью (рис. 2).

Рис. 2. Структурная схема следящей системы

Исходные соотношения:

– ошибка слежения. (1)