Реферат: Логарифмические частотные характеристики и передаточные функции радиотехнической следящей системы
Метод логарифмических частотных характеристик (ЛЧХ) используется как для анализа, так и для синтеза следящих систем. Метод построения ЛЧХ состоит в графическом изображении АЧХ и ФЧХ в логарифмическом масштабе. Особенно удобен метод, использующий асимптотические логарифмические амплитудно-частотные характеристики (ЛАЧХ). Для некоторых систем, называемых мимнимально-фазовыми, достаточно построить лишь ЛАЧХ, так как она определяет все свойства системы. К минимально-фазовым относят системы, у которых корни характеристических уравнений, составленных из числителя и знаменателя передаточной функции имеют отрицательные вещественные части.
Метод построения асимптотических ЛАХ состоит в следующем. Выражение для ЛАЧХ и ЛФЧХ записываются в виде
Частота откладывается по оси абсцисс в логарифмическом масштабе, а усиление – в децибелах (дБ) по оси ординат. Логарифмическая фазочастотная характеристика (ЛФЧХ) строится под ЛАЧХ с общей осью частот.
Метод построения асимптотических ЛАХ рассмотрим на примере.
Пусть передаточная функция разомкнутой системы определяется выражением
.
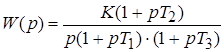Заменой переменной перейдем к частотной передаточной функции
,
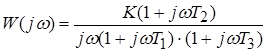где Т1 , Т2 , Т3 – постоянные времени соответствующих звеньев; К – коэффи циент усиления или добротность (имеет размерность частоты).
Модуль частотной передаточной функции А(ω) последовательно включенных звеньев определяется как произведение модулей этих звеньев. а аргумент – как сумма фазовых сдвигов звеньев.
;
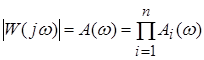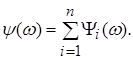
Обычно полагают, что 
. Пусть Т1 > Т2 , > Т3 .
Обозначим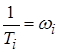 
– сопрягающая частота; 
. Тогда
;
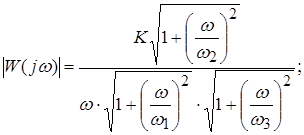
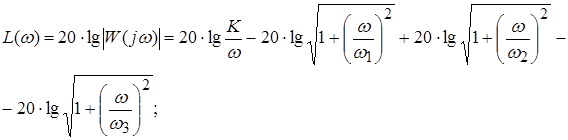
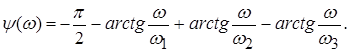При построении асимптотических ЛАХ используется следующее правило:
Если 
, то пренебрегают вторым слагаемым, т.е. 
.
Если 
, то пренебрегают единицей,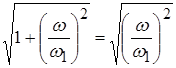 
При этом в точке сопряжения ошибка не превышает нескольких дБ.
Асимптотическая ЛАХ для n последовательно включенных звеньев состоит из n+1 асимптоты, каждая из которых строится в диапазоне частот:
1ая: 
;
2ая: 
;
… … … … …
n+1: 
.
Построим L(ω) (рис. 1).
Уравнение для первой асимптоты ():
--> ЧИТАТЬ ПОЛНОСТЬЮ <--