Реферат: Логіка і множини
Якщо вжити Т "true" для позначення істинного вислову і F"false" для хибного, вище наведені означення можуть бути представлені у вигляді таблиці істинності "truthtable":

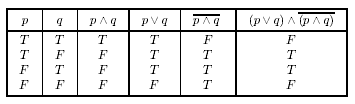
Приклад 1 Побудуємо таблицю істинності для більш складної логічної конструкції ![]()
3. Тавтологія і логічна еквівалентність
Означення 1. Тавтологія це істинний в логічному значенні вислів.
Важко привести приклад елементарної пропозиції, яку б можна було назвати тавтологією. Як правило це поняття характерне для складних пропозицій і означає, які б не були логічні значення складових пропозицій, складна пропозиція завжди буде істинною, якщо вона є тавтологією. Всі можливі комбінації логічних значень складових називаються інтерпретаціями. Вище наведені таблиці істинності показують, що для двох складових існує всього 4 інтерпретації. Якщо трохи подумати, то прийдемо до висновку, що три складові мають 23 = 8 інтерпретацій і взагалі, n складових мають 2n інтерпретацій. Використовуючи цей термін можна перефразувати означення 1.1 як : тавтологія – це пропозиція істинна при всіх інтерпретаціях її складових. Керуючись цим означенням легко довести істинність наступних пропозицій:
Приклад 1. Вислови
![]()
![]()
є тавтології. Це дає можливість писати p∧q∧rбез дужок, узагальнивши поняття кон’юнкції для більше ніж двох висловів.
Приклад 2. Вислови
![]()
![]()
є тавтології. Це дає можливість писати pÚqÚrбез дужок, узагальнивши поняття диз’юнкції для більше ніж двох висловів.
Приклад 3. Вислівp∨pє тавтологія.
Приклад 4. Вислів (p→q) «(q→p) є тавтологія.
Приклад 5. Вислів (p→q) «(p∨q) є тавтологія.
Приклад 6. Вислів (p«q) «((p∨q)∧(p∧q)) є тавтологія; про що свідчить наступна таблиця істинності:

Пропонуємо студентам довести, що наступні вислови є тавтології.
Розподільний закон.
(a) (p∧(q∨r)) «((p∧q) ∨(p∧r)); (b) (p∨(q∧r)) «((p∨q) ∧(p∨r)).
Закон де Моргана.
(a) (p ∧q) «(p ∨q); (b) (p ∨q) «(p ∧q).
Правила виводу.
(a) (MODUS PONENS) (p ∧(p →q)) →q;
(b) (MODUS TOLLENS) ((p →q) ∧q) →p;
(c) (SYLLOGISM) ((p →q) ∧(q →r)) →(p →r).