Реферат: Математическая логика и теория алгоритмов
1. Постановка задачи.
2. Построение модели.
3. Описание алгоритма
4. Доказательство правильности алгоритма
5. Блок-схема алгоритма
6. Описание переменных и программа
7. Расчёт вычислительной сложности
8. Тестирование
9. Список литературы
Постановка задачи.
Перечислить все способы расстановки n ферзей на шахматной доске n на n, при которых они не бьют друг друга.
Построение модели.
Очевидно, на каждой из n горизонталей должно стоять по ферзю. Будем называть k-позицией (для k = 0, 1,...,n) произвольную расстановку k ферзей на k нижних горизонталях (ферзи могут бить друг друга). Нарисуем "дерево позиций": его корнем будет единственная 0-позиция, а из каждой k-позиции выходит n стрелок вверх в (k+1)-позиции. Эти n позиций отличаются положением ферзя на (k+1)-ой горизонтали. Будем считать, что расположение их на рисунке соответствует положению этого ферзя: левее та позиция, в которой ферзь расположен левее.
Дерево позиций для n = 2
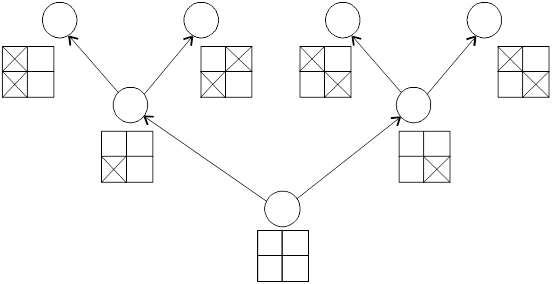
Данное дерево представлено только для наглядности и простоты представления для n=2.
Среди позиций этого дерева нам надо отобрать те n-позиции, в которых ферзи не бьют друг друга. Программа будет "обходить дерево" и искать их. Чтобы не делать лишней работы, заметим вот что: если в какой-то k-позиции ферзи бьют друг друга, то ставить дальнейших ферзей смысла нет. Поэтому, обнаружив это, мы будем прекращать построение дерева в этом направлении.
Точнее, назовем k-позицию допустимой, если после удаления верхнего ферзя оставшиеся не бьют друг друга. Наша программа будет рассматривать только допустимые позиции.
Описание алгоритма.
Разобьем задачу на две части: (1) обход произвольного дерева и (2) реализацию дерева допустимых позиций.
Сформулируем задачу обхода произвольного дерева. Будем считать, что у нас имеется Робот, который в каждый момент находится в одной из вершин дерева. Он умеет выполнять команды:
вверх_налево (идти по самой левой из выходящих вверх стрелок)
вправо (перейти в соседнюю справа вершину)
вниз (спуститься вниз на один уровень)
вверх_налево
вправо
вниз
и проверки, соответствующие возможности выполнить каждую из команд, называемые "есть_сверху", "есть_справа", "есть_снизу" (последняя истинна всюду, кроме корня). Обратите внимание, что команда "вправо" позволяет перейти лишь к "родному брату", но не к "двоюродному".
Будем считать, что у Робота есть команда "обработать" и что его задача - обработать все листья (вершины, из которых нет стрелок вверх, то есть где условие "есть_сверху" ложно). Для нашей шахматной задачи команде обработать будет соответствовать проверка и печать позиции ферзей.
Доказательство правильности приводимой далее программы использует такие определения. Пусть фиксировано положение Робота в одной из вершин дерева. Тогда все листья дерева разбиваются на три категории: над Роботом, левее Робота и правее Робота. (Путь из корня в лист может проходить через вершину с Роботом, сворачивать влево, не доходя до нее и сворачивать вправо, не доходя до нее.) Через (ОЛ) обозначим условие "обработаны все листья левее Робота", а через (ОЛН) - условие "обработаны все листья левее и над Роботом".
Нам понадобится такая процедура:
procedure вверх_до_упора_и_обработать
{дано: (ОЛ), надо: (ОЛН)}
--> ЧИТАТЬ ПОЛНОСТЬЮ <--