Реферат: Математическая логика и теория алгоритмов

while есть_снизу do begin

if есть_справа then begin {ОНЛН, есть справа}

вправо;

{ОНЛ}

вверх_до_упора_и_обработать;

end else begin

{ОЛН, не есть_справа, есть_снизу}

вниз;

обработать;

end;

end;

{ОНЛН, Робот в корне => все вершины обработаны полностью}

Доказательство правильности алгоритма.

Докажем , что приведенная программа завершает работу (на любом конечном дереве).

Доказательство . Процедура вверх_налево завершает работу (высота Робота не может увеличиваться бесконечно). Если программа работает бесконечно, то, поскольку листья не обрабатываются повторно, начиная с некоторого момента ни один лист не обрабатывается. А это возможно, только если Робот все время спускается вниз. Противоречие.

Блок-схема алгоритма.

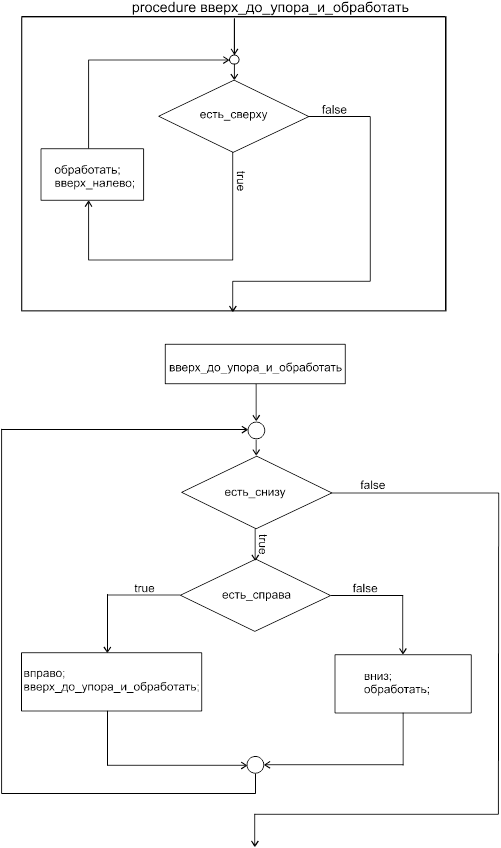Описание переменных и программа.

Теперь реализуем операции с деревом позиций. Позицию будем представлять с помощью переменной k: 0..n (число ферзей) и массива c: array [1..n] of 1..n (c [i] - координаты ферзя на i-ой горизонтали; при i > k значение c [i] роли не играет). Предполагается, что все позиции допустимы (если убрать верхнего ферзя, остальные не бьют друг друга).

program queens;

const n = ...;

var k: 0..n;

c: array [1..n] of 1..n;

procedure begin_work; {начать работу}

begin

k := 0;

end;

function danger: boolean; {верхний ферзь под боем}

var b: boolean;

i: integer;

begin

if k <= 1 then begin

danger := false;