Реферат: Математическая Логика
11) 
Reg – правила вывода ИВ (некоторые правила преобразования первого слова в другое).
a – символ переменной 
- произвольное слово ИВ (формула)
Отображение 
действует так, что на место каждого вхождения символа а , пишется слово .
Пример: 
Правило modus ponens : 
3.1.2 Формальный вывод. (простейшая модель доказательства теоремы)
Опр: Последовательность формул ИВ, называется формальным выводом, если каждая формула этой последовательности имеет следующий вид:
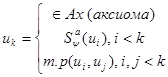
Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в какой-нибудь формальный вывод. 
- выводимая формула ИВ.
Пример: 
| 1) |  |  |
| 2) |  |  |
| 3) |  |  |
| 4) |  |  |
| 5) |  |  |
| 6) |  |  |
Правило одновременной подстановки.
Замечание : Если формула 
выводима, то выводима и 
Возьмем формативную последовательность вывода 
и добавим в неё 
, получившаяся последовательность является формальным выводом.
(Если выводима то если 
, то выводима 
)
Теор: Если выводимая формула , то 
(
- различные символы переменных) выводима
Выберем 
- символы переменных которые различны между собой и не входят не в одну из формул 
, сделаем подстановку 
и последовательно применим 
и в новом слове делаем последовательную подстановку: 
, где 
- является формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез 
(формулы), называется такая последовательность слов 
, каждая из которых удовлетворяет условию:
если формулу можно включить в некоторый формальный вывод из гипотез .
Лемма: ; 
: то тогда 
Напишем список:
Лемма :
Док:
3.1.4 Теорема Дедукции.
Если из