Реферат: Математическая Логика

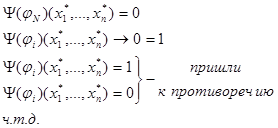
(1)

3.3 Непротиворечивость ИВ.

3.3.1 Определение.

1) ИВ противоречиво , если формула А выводима в нем. .

2) формула выводима в ИВ)ИВ противоречиво .

3) ИВ противоречиво .

ИВ непротиворечиво , если оно не является противоречивым.

Теорема : ИВ является непротиворечивым исчислением по отношению к любому из трех определений.

Док-во : (1) Если , то соответствующая ей булева функция будет тождественно равна 1.

(2) Если любая формула выводима, то выводима и А , что соответствует пункту 1.

(3) Пусть и - булева функция

- противоречие.

3.4 Формальные исчисления.

Алфавит – конечное или счетное множество символов, возможно, разбитых на группы. Алфавит должен быть упорядоченным множеством.

Слово – конечная упорядоченная последовательность символов алфавита, в т.ч. пустое слово.

V – множество всех слов.

Вычислимая функция от нескольких натуральных переменных

( f – может быть не всюду определенной )

f – называется вычислимой , если такая машина Тьюринга, которая её вычисляет.

- разрешимое множество, если характеристическая функция

- является вычислимой.

Множество называется перечислимым, если такая вычислимая функция

М - разрешимо М и N \M перечислимы.

М – перечислимо М – область определения некоторой вычислимой функции.

Множество всех формул F – некоторое разрешимое подмножество V .

Т – счетное множество, если его биективное отображение на V .

- обозначение счетного множества. ( - алеф-нуль)