и ее ранг rank2, то есть настоящая система полностью управляема по состояниям.

Задача 4.2.2

Определить управляемость по выходам динамической системы, заданной векторными уравнениями

,

.

Решение.

В соответствии с выражением (4.1.2) запишем матрицу управляемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2

.

Найдем произведение матриц

.

.

Следовательно, матрица управляемости имеет вид

,

и ее ранг rank=2, то есть настоящая система полностью управляема по выходам.

5. НАБЛЮДАЕМОСТЬ

5.1. ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

Наблюдаемость системы (2.1.1), (2.1.2) определяется теоремой (критерием) Калмана: система будет вполне наблюдаемой тогда и только тогда, когда ранг матрицы наблюдаемости L₀ размерности равен n, то есть

rankn, (5.1.1)

где

. (5.1.2)

Если rank<n, то система будет не вполне наблюдаемой, а при rank=0 – полностью ненаблюдаемой.

5.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 5.2.1

Определить наблюдаемость динамической системы, заданной векторными уравнениями

.

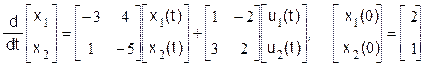
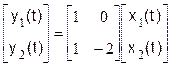Решение.

В соответствии с выражением (5.1.2) запишем матрицу наблюдаемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2

.

Найдем произведение матриц

.

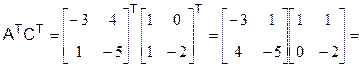
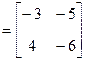Следовательно, матрица наблюдаемости имеет вид

,

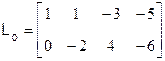и ее ранг rank2, то есть настоящая система полностью наблюдаема.