Реферат: Математическая теория захватывания

Запишем уравнение, определяющее эти P и Q, т.е. соотношение (31) для нашего случая.

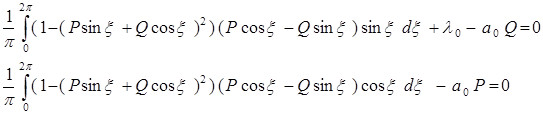
Или преобразовав их, получим следующее:

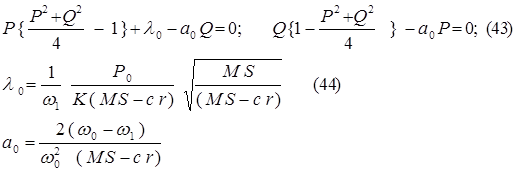
Полагая Р = R sin j; Q = R cos j. Далее найдем для амплитуды R и фазы j для того исходного периодического решения, в близости к которому устанавливается рассматриваемое периодическое решение , соотношения связывающие их :

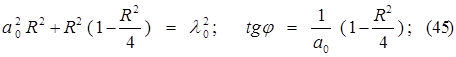
Первая формула дает "резонансную поверхность" для амплитуды. Вторая - для фазы. По (38) условия устойчивости имеют вид b < 0, D> 0. Считаем b и D через формулы (35-37).

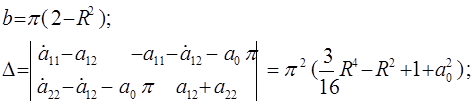
(46)

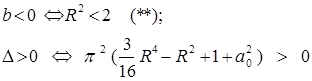
Т.е. решение является устойчивым, если удовлетворяется условие (**). В заключение выпишем формулы для вычисления a_о, соответствующего ширине захватывания для рассматриваемого случая.

1)

a₀ - является общим корнем уравнений

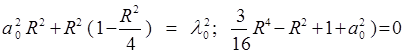
2)

Сама ширина Dw, отсчитанная от одной границы захватывания до другой выражается следующим образом: Dw = a_о w² _о (MS - c r). Можно дать простые формулы для вычисления ширины захватывания в следующих случаях:

а) l² _о << 1; Dw = w_о Р_о /V^о _g .

б) для очень сильных сигналов 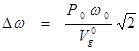( V^о _g - амплитуда сеточного напряжения при отсутствии внешней силы).

Список литературы

1. Андронов А.А. Собрание трудов, издательство "Академии наук СССР", 1956.

2. Андронов А.А., Витт А. К теории захватывания Ван дер Поля. . Собрание трудов, издательство "Академии наук СССР", 1956.

3. Ляпунов А. Общая задача об устойчивости движения, Харьков, 1892.