Реферат: Математические методы экономики
В условиях рыночной системы управления производственной и сбытовой деятельностью предприятий и фирм в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе основой предпринимательской деятельности становится изучение потребительского спроса.
Рассмотрим некоторые вопросы моделирования спроса и потребления.
Уровень потребления общества можно выразить целевой функцией потребления U = U(Y), где Y ![]() О - вектор переменных разнообразных товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую интерпретацию уравнений U(Y) = С, где С - меняющийся параметр, характеризующий значение (уровень) целевой функции потребления (например, доход или уровень материального благосостояния).
О - вектор переменных разнообразных товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую интерпретацию уравнений U(Y) = С, где С - меняющийся параметр, характеризующий значение (уровень) целевой функции потребления (например, доход или уровень материального благосостояния).
В совокупности потребительских благ каждому уравнению U(Y) = С соответствует определенная поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. Для наглядности рассмотрим пространство двух благ, например, в виде двух агрегированных групп товаров: продукты питания (y1 ) и непродовольственные товары, включая услуги (у2 ). Тогда уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям С (рис. 8.1, где С1 < С2 < Сз).
|
|
Рис. 8.1. График кривых безразличия
Из основных свойств целевой функции потребления можно отметит следующие:
1. функция U(Y) является возрастающей функцией всех своих аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции;
2. кривые безразличия не могут пересекаться, т.е. через одну точку совокупности благ (товаров, услуг) можно провести только одну поверхность безразличия;
3. кривые безразличия имеют отрицательный наклон к каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.
Методы построения целевой функции потребления основаны на обобщении опыта поведения потребителей и тенденций покупательского спроса в зависимости от уровня благосостояния.
Рассмотрим моделирование поведения потребителей в условиях товарно-денежных отношений на базе целевой функции потребления. В основе модели поведения потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей.
Пусть в совокупности п видов товаров исследуется поведение потребителей. Обозначим спрос потребителей через вектор Y = (y1 , у2 ,...,yn ), а цены на различные товары - через вектор Р = (р1 , р2 ,…,pп ). Пусть D - величина дохода. Тогда потребители могут выбирать только такие комбинации товаров, которые удовлетворяют ограничению 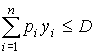 , называемому бюджетным ограничением.
, называемому бюджетным ограничением.
Пусть U(Y) целевая функция потребления. Тогда простейшая модель поведения потребителей в векторной форме можно записать в виде:
![]() (8.1)
(8.1)
Геометрическая интерпретация модели (8.1) для двух агрегированных групп товаров представлена на рис. 8.2.
Линия АВ (в других вариантах А1 В1 , А2 В2 ) соответствует бюджетному ограничению и называется бюджетной линией. Выбор потребителей ограничен треугольником АОВ (A1 OB1 , A2 OB2 ).
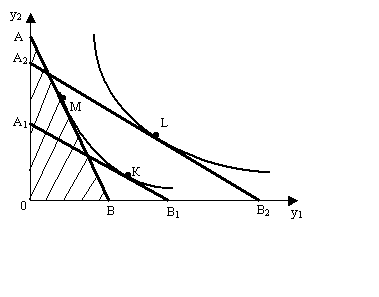
Рис. 8.2. График простейшей модели поведения потребителя
Набор товаров М, соответствующий точке касания прямой АВ с наиболее отдаленной кривой безразличия, является оптимальным решением (в других вариантах это точки К и L). Легко заметить, что линии АВ и A1 B1 соответствуют одному и тому же размеру дохода и разным ценам на товары y1 и у2 ; линия A2 B2 соответствует большему размеру дохода.
На основе теории нелинейного программирования, можно определить математические условия оптимальности решений для модели (8.1). С задачей нелинейного программирования связывается так называемая функция Лагранжа, которая для задачи (8.1) имеет вид
L(Y, l,) = U(Y) + l(D - PY),
где множитель Лагранжа l является оптимальной оценкой дохода.
Обозначим частные производные функции U(Y) через Ui : ![]()
Они представляют собой предельные полезные эффекты (предельные полезности) соответствующих потребительских благ и показывает на сколько единиц увеличивается целевая функция потребления при увеличении использования i- гоблага (товара) на некоторую условную «малую единицу».
Необходимыми условиями того что вектор Y0 будет оптимальным решением, является условия Куна-Таккера:
![]()
при этом![]()
![]() (товар приобретается)
(товар приобретается)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--