Реферат: Математические модели формирования и использования запасов

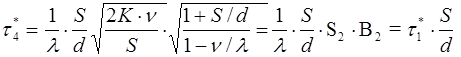
Подставив τ₂ ^* и τ₂ ^* в формулы (4-5) и (4-4), получим оптимальные значения цикла повторения заказа и партии однопродуктовой поставки:

τ_ц ^* =√ 2·K/(S·n)·√(1+ S / d)/ (1-n/l)= S₁ /B₁ (4-17)

q^* = √ 2·K·n/S·√(1+ S / d)/ (1-n/l)= S₂ /B₁ (4-18)

Аналогично, подставив значения τ₂ ^* и τ₃ ^* из (4-13) и (4-14) в (4-9), определим оптимальные удельные издержки системы:

L_уд ^* =√ 2·K·n·S√ (1-n/l)/(1+ S / d)= √ 2·K·n·S· B₁ (4-19)

И, наконец, находим оптимальные значения максимального уровня наличного запаса и задолженного спроса:

Y^* = √ 2·K·n/S·√ (1-n/l)/(1+ S / d)= √ 2·K·n/(S · B₁ ) (4-20)

y^* = S / d·√ 2·K·n/S·√ (1-n/l)/(1+ S / d)= S / d·√ 2·K·n/(S · B₁ ) (4-21)

Общие оптимальные издержки системы за время возобновления запаса составят:

L_общ ^* = L_уд ^* ·τ_ц ^* (4-22)

Модель с учетом неудовлетворенных требований при конечной интенсивности поступлений можно широко применять при:

1. управлении поставками материальных ресурсов;

2. определении оптимальной величины запуска деталей в производство с учетом переналадок на одном и том же технологическом оборудовании.

Во втором случае K – это издержки, связанные с переналадками. Предполагается, что они не зависят от величины выпускаемой партии и порядка запуска деталей в производство, l – интенсивность выпуска (производительность), τ₁ + τ₄ – время, затраченное на производство определенного типа изделий.

Из уравнений (4-13) – (4-22) можно получить ряд других частных моделей:

a) при большой интенсивности пополнения, когда вся заказанная партия поступает одновременно; это значит, что l>>n и тогда можно принять n/l®0.

b) при больших штрафах за допущение дефицита S/d®0, т.е. дефицит недопустим (d>>S).

c) когда пункты а) и b) действуют одновременно. т.е. n/l®0, S/d®0, тогда имеем:

q^* = √ 2·K·n/S

τ_ц ^* =√ 2·K/(S·n)

L_уд ^* =√ 2·K·n·S

Последняя модель в отечественной и зарубежной литературе получила название Уилсона .Применяя формулы (4-17) – (4-19), можно показать, что за счет разумного компромисса между затратами на содержание и потерями от дефицита можно уменьшить общие затраты в единицу времени в √ 1+S/d раз. При n/l®0 и высоких штрафах за дефицит рассматриваемая модель превращается в модель Уилсона.

1.2 Оптимальные партии поставки для многопродуктовых моделей

Также как и для однопродуктовых поставок, суммарные издержки от функционирования системы складываются из издержек размещения заказов, содержания запаса и убытков вследствие дефицита.

Суммарные издержки размещения заказа:

∑_i К_i = К₀ (1+ γ·N)

где К₀ – издержки, не зависящие от числа одновременно заказанных продуктов и размера партии поставки;

γ – доля издержек, учитывающая размещение заказа по каждому i-тому продукту;

N – число продуктов.