Реферат: Математическое програмирование
![]()
![]()
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае -57 минимально, поэтому в качестве разрешающего элемента выбирается второй элемент второго столбца – 2 (выделен в таблице).
Шаг 3: Вторая строка таблицы делится на 2
От элементов строки 1 отнимает соответствующие элементы строки 2, умноженные на 2.
От элементов строки 3 отнимает соответствующие элементы строки 2.
От элементов строки 4 отнимает соответствующие элементы строки 2, умноженные на -3.
| Базис | Cб | В | 2 | 3 | 0 | 0 | 0 |
| А1 | А2 | А3 | А4 | А5 | |||
| А3 | 0 | 10 | 1 | 0 | 1 | - | 0 |
| А5 | 0 | 19 | 0,5 | 1 | 0 | 0,5 | 0 |
| А2 | 3 | 35 | 2,5 | 0 | 0 | -0,5 | 1 |
| Fi - Ci | 57 | -0,5 | 0 | 0 | 1,5 | 0 |
Таким образом, новыми базисными переменными становятся А3 , А5 , А2 .
Возвращаемся к шагу 1 и повторяем весь процесс.
Проверяется критерий оптимальности. Отрицательная оценка только одна – в столбце А1 .
Вычисляем:
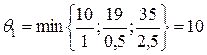
Разрешающим элементом будет первый элемент первого столбца – 1.
Новыми базисными переменными становятся A5 , A2 , A1
От элементов строки 2 отнимает соответствующие элементы строки 1, умноженные на 0,5.
От элементов строки 3 отнимает соответствующие элементы строки 1, умноженные на 2,5.
От элементов строки 4 отнимает соответствующие элементы строки 1, умноженные на -0,5.
| Базис | Cб | В | 2 | 3 | 0 | 0 | 0 |
| А1 | А2 | А3 | А4 | А5 | |||
| А5 | 0 | 10 | 1 | 0 | 1 | -1 | 0 |
| А2 | 3 | 14 | 0 | 1 | -0,5 | 1 | 0 |
| А1 | 2 | 10 | 0 | 0 | -2,5 | 2 | 1 |
| Fi - Ci | 62 | 0 | 0 | 1,5 | 1 | 0,5 |
Отрицательных оценок нет, то есть критерий оптимальности выполнен.
Таким образом, получается искомое значение целевой функции
F(10; 14; 0; 0; 10) = 62, т.е. возвращаясь к системе неравенств, получаем:
![]()
Ответы, полученные различными методами, совпадают.
Ответ: хопт = ( 10 , 14) Значение функции : F = 62
Задача 2
Имеются три пункта отправления А1 ,А2 ,А3 однородного груза и пять пунктов В1 , В2 , В3 , В4 , В5 его назначения. На пунктах А1 ,А2 ,А3 находится груз в количествах 50, 30, 70 тонн. В пункты В1 , В2 , В3 , В4 , В5 требуется доставить соответственно 20, 30, 50, 30, 20 тонн груза. Расстояния в сотнях километрах между пунктами отправления и назначения приведены в матрице D:
Пункты отправления | Пункты назначения | ||||
| В1 | В2 | В3 | В4 | В5 | |
| А1 | 9 | 5 | 1 | 1 | 9 |
| А2 | 7 | 1 | 4 | 9 | 4 |
| А3 | 5 | 3 | 4 | 9 | 9 |
Найти такой план перевозок, при котором общие затраты на перевозку грузов будут минимальными.
Указания: 1) считать стоимость перевозок пропорциональной количеству груза и расстоянию, на которое этот груз перевозится, т.е. для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах;
2) для решения задачи использовать методы северо-западного угла и потенциалов.
Решение.
Составим математическую модель задачи: