Реферат: Методи розрахунку аберацій оптичної системи

Під цими даними в колонках наводяться конструктивні параметри оптичної системи: радіуси r , відстані d між вершинами поверхонь уздовж оптичної осі, показники переломлення n для основної довжини хвилі, коефіцієнти дисперсії і марки скла.

У наступних колонках на рядках радіусів указуються світлові і повні діаметри оптичної поверхні. У деяких випадках наводяться і стрілки по світловому і повному діаметрі кожної поверхні.

Рисунок 2 – Графіки аберацій дволінзового склеєного об'єктива:

а ) подовжньої сферичної аберації для трьох хвиль; б) хроматизму положення; в ) що характеризують сагитальну і меридіональну кривизну поверхні зображення; г) дисторсії; д) поперечної сферичної аберації для трьох хвиль; е, ж) поперечної аберації широкого похилого пучка в меридіональному перетині для трьох довжин хвиль для зони і краю поля відповідно; з, и) сагітальної складової поперечної аберації широкого сагітального пучка для зони і краю поля відповідно.

Після конструктивних параметрів звичайно наводиться текстовий матеріал, у якому вказуються додаткові зведення, наприклад, рівняння асферичних поверхонь, якщо вони присутні в оптичній системі, положення апертурної діафрагми, положення площин вхідної і вихідної зіниці, збільшення в зіницях і т.п.

Результати обчислень для всіх променів кожного пучка для заданих довжин хвиль зводяться в таблиці, що розташовуються в правій частині формату.

За даними розрахунку будують графіки залишкових аберацій (рис. 2), що є складовою частиною оптичного випуску. З рис. 2, б випливає, що в об'єктиві хроматизм положення недовиправлений. З рис. 2, а, д видно, що в об'єктиві для всіх променів, що йдуть через край вхідної зіниці, сферична аберація «пере виправлена». Сферохроматизм для довжин хвиль – і виправлений для променя, що йде вище зонального. Розмір кружка розсіювання для точки на осі визначається променями, що проходять через краї вхідної зіниці. Кружок для основної довжини хвилі визначається величиною = 0,02 мм, а в розглянутому спектральному діапазоні діаметр кружка = 0,034 мм.

На підставі розглянутих графіків можна зробити висновок, що в оптичній системі велика аберація кривизни як у меридіональному, так і в сагітальних перетинах, а дисторсія мала.

Графіки аберацій широких похилих пучків у меридіональному перетині представлені на рис. 2, е, ж для зони і краю поля відповідно. Як випливає з цих графіків, розмір плями розсіювання в меридіональному перетині визначається променями основної довжини хвилі, що проходять через верхній і нижній краї вхідної зіниці. Вибираючи відповідні величини, отримаємо розмір плями в меридіональному перетині для зони поля 0,058 мм, а для краю поля 0,136 мм. Найбільший внесок у розмір цієї плями вносить кривизна поля – нахил характеристичних кривих на початку координат.

З рис. 2, и видно, що розмір плями розсіювання в сагітальному перетині визначається крайніми променями і дорівнює = 0,054 мм.

Зсув площини установки для даного об'єктива не дасть істотного зменшення плями розсіювання, тому що припереміщенні площини зображення убік об'єктива розмір плями розсіювання для похилих пучків зменшуватиметься, а пляма розсіювання в центрі поля збільшуватиметься на таке ж саме значення.

2. Підсумовування аберацій

аберація оптичний промінь об'єктив

Звичайно при розрахунку складної оптичної системи її розбивають на окремі вузли, розрахунок яких здійснюється по програмах автоматизованого розрахунку, або ці вузли вибирають з каталогів оптичних випусків раніше розрахованих оптичних систем. Для визначення аберацій усієї системи проводять підсумовування аберацій від кожного вузла в загальній площині зображення. Попередньо необхідно переконатися в тому, чи є вихідні характеристики кожного попереднього вузла, тому що площина зображення, формована попереднім вузлом, є предметною для наступного компонента; поле в просторі зображення попереднього вузла відповідає полю в просторі предметів наступного; вихідна зіниця попереднього вузла є вхідною зіницею наступного (апертурний кут у просторі зображень попереднього вузла дорівнює апертурному куту в просторі предметів наступного).

Відомо, що аберації оптичної системи можна розділити на дві групи: подовжні аберації, що обчислюються уздовж оптичної осі, і поперечні аберації, що обчислюються в напрямку, перпендикулярному оптичній осі системи.

Розглянемо підсумовування подовжніх аберацій. Якщо попередній вузол має подовжню аберацію , то від дії наступного k-го вузла відповідно до формули (***) зв'язку між подовжнім і лінійним збільшеннями ця аберація стане рівною , до якої додасться аберація k- го вузла. У підсумку сумарна аберація після k-го вузла буде

. (1)

Якщо система складається з р вузлів (компонентів), то на основі формули (1) сумарна подовжня аберація всієї системи

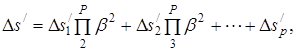(2)

де – добуток квадратів лінійних збільшень усіх компонентів від2-го до р- го.

При підсумовуванні поперечних аберацій для k- го компонента отримаємомо, що

, (3)

а для оптичної системи з р компонентів, використовуючи формулу (3), знайдемо

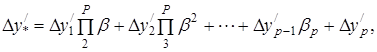(4)

Слід зазначити, що при використанні формул (1) і (2) підсумовування має виконуватися по ходу одного променя.

Аберації окремих вузлів розраховують за умови, що зображення знаходиться над оптичною віссю (у' >0). Однак при компонуванні системи ця умова не завжди виконується. Це призводить до зміни знаків у поперечних абераціях. Тому у формулах (3), (4) варто враховувати знак лінійного збільшення.

Оптичні системи можуть включати компоненти, між якими промені мають рівнобіжний хід. У таких системах проміжні площини зображення розташовані в передній фокальній площині одного компонента й у задній фокальній площині іншого компонента. Для цих систем формули (3), (4) незастосовні, тому що для першого з цих компонентів лінійне збільшення має нескінченно велике значення, а для другого b = 0 . У цьому випадку для першого компонента аберації вираховують у зворотному ході променів (,), а для другого – у прямому ході променів. Потім ці два компоненти розглядають як один компонент із лінійним збільшенням ( і – переднє і заднє фокусні відстані компонентів). Аберації такого складного компонента обчислюють за такими формулами:

, (5)