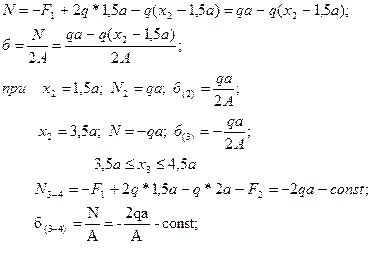Реферат: Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов

Изобразим сечение в масштабе, укажем центры тяжести составляющих фигур и переведем главные центральные оси составляющих фигур (рис. 2.2).

За исходные оси (оси, в которых будет определяться центр тяжести) примем главные центральные оси фигуры «2» (рис. 2.2). Определяем координаты Yc и Zc центра тяжести всей фигуры «с» в выбранной исходной системе координат Y2C2Z2. Так как ось У2 – ось симметрии всей фигуры, то центр тяжести лежит на оси Уz и Zc = 0. Координата Ус равна (рис. 2.2).

Откладываем отрезки Ус = - 3,48 и Zc=0 и отмечаем центр тяжести «С» (рис2.2).

Проверка правильности определения центра тяжести проводится аналогично решению примера 1, пункт 1.

2. Определение положения главных осей.

Заданное сечение имеет ось симметрии Ус. Следовательно, центробежный момент - главные. А так как «С» центр тяжести, то оси Ус и Zc – главные центральные.

3. Определение величины главных центральных моментов инерции .

Смещение центров тяжести составляющих фигур относительно осей Ус и Zc показано на рис. 2.2:

Значения моментов инерции составляющих фигур относительно собственных главных осей приведены в разделе 1.

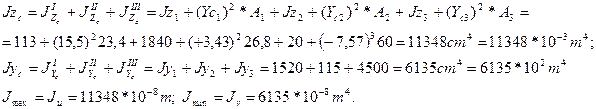
ПРИМЕР 3

Для изображенной на рис. 3.1 схема стального бруса требуется:

1) построить эпюры продольных сил N и нормальных напряжений б, записав в общем виде для каждого участка выражения N и б и указа на эпюрах их значения в характерных сечениях;

2) установить опасное сечение и записать условие прочности. Определить размеры прямоугольного сечения бруса, приняв h/b=2?0;

3) найти перемещения сечения 2.

Исходные данные:

Для выполнения числовых расчетов принять: (для студентов строительных специальностей принять R=210МПа)

РЕШЕНИЕ

1. Изобразим в масштабе расчетную схему бруса (рис. 3.2ба) с учетом знаков исходных данных (если нагрузка задана со знаком минус, то ее на схеме следует направить в противоположную сторону). Построим эпюры N и б, рассматривая каждый участок, начиная со свободного конца. Используя метод сечений, разрежем брус некоторым сечением с ординатой (участок 1-2), изобразим нижнюю часть бруса отдельно, отбросив верхнюю часть и заменив ее действие продольной силой N (рис. 3.2,б).

Запишем уравнение равновесия и найдем силу N:

- уравнение наклонной прямой.

Мысленно выполняя приведенные выше операции метода сечений для каждого участка, запишем выражения для N и б: участок 1-2:

- уравнение наклонной прямой;

- уравнение наклонной прямой при

участок 2-3;