Реферат: Методика изучения числовых систем

Рис. 2.

???.1.

Рис. 3. Рис. 4

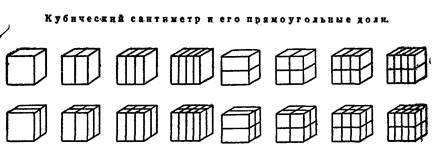
В результате такой работы у учащихся создается отчетливое представление о дроби как совокупности равных долей единицы, и сами учащиеся составляют соот­ветствующее определение. Мно­гие учебники сразу же рассматри­вают второй способ получения дроби при делении целого числа на равные части. На ряде кон­кретных примеров показывают, что при делении меньшего числа на большее получается в частном одна или несколько долей единицы, т.е., согласно ранее веденному определению, рассуждения ведутся Рис. 5. так.

????? ????????? ??????? ??????? ? 3 ? ?? 4 ?????? ?????, ????? ????????

Рис. 6.

представить каждый метр веревки разделенным на 4 равные части, тогда веревка будет содержать 12 четвертей метра, разделив 12 четвертей метра на 4 равные части, получим в каждой метра. Это рассуждение иллюстрируется рисунком 6.

Рассматривается второй способ рассуждений: чтобы делить 3 яблока (или 3 листа бумаги) 4 детям, можно каждое яблоко разделить на 4 равные части и каждому дать по одной четверти. Каждый ребенок получит яблока.

Основная мысль приведенных рассуждений та, что доли единицы можно взять за новые счетные единицы и с полученными числами производить действия так же, как, с целыми именованными числами. Но почему же начинать с деления? Деление определяется как дей­ствие, обратное умножению. Удовлетворяет ли рассмотренное деление этому определению? 3 : 4 = ; ·4 будет ли равно 3? Все это требует обоснования. Без этого учащиеся не будут связывать этот случай деления с определением деления.

После того как введено понятие дроби, необходимо ввести по­нятия равенства и неравенства дробей. В теоретических курсах эти понятия вводятся путем определений. В школьном курсе необходимо показать предварительно целесообразность вводимых определений путем рассмотрения конкретных примеров.

Составляя дроби из долей одной и той же единицы, учащиеся убеждаются, что дроби могут быть меньше единицы, равны единице, больше единицы. Эти наблюдения и следует положить в основу определений и классификации дробей на неправильные и правиль­ные. Формальный же признак, указывающий на соотношение между числителем и знаменателем у правильных и неправильных дробей, следует установить, как следствие определения. Обращение сме­шанного числа в равную ему неправильную дробь и исключение целого числа из неправильной дроби следует начать с рассмотрения конкретных примеров. При составлении отрезков из долей линейной единицы, возникает вопрос: сколько целых линейных единиц содер­жится в данном отрезке? При составлении прямоугольников из долей квадратной единицы возникает вопрос: сколько квадратных единиц можно составить из данного прямоугольника? Решение этих вопро­сов приводит к исключению целого числа из неправильной дроби.

Не следует спешить с выводом формального правила для этих, преобразований, следует заставлять учащихся проводить соответ­ствующие рассуждения, основанные на составе единицы из долей этой единицы. Например, при обращении смешанного числа 2 в неправильную дробь ведутся следующие рассуждения:в единице 3 третьих доли, в двух единицах 3· 2 третьих долей, всего (3·2+2).

Отсюда

В методической литературе поднимался вопрос о включении в школьный курс обращения смешанного числа в неправильную дробь и обратного преобразования после изучения деления дроби на целое число и деления дробей с одинаковыми знаменателями, так как при первом преобразовании производится умножение дроби на целое число и сложение дробей, при втором — деление дробей с одинаковыми знаменателями. Но принятое обычно расположение материала имеет преимущество: возможно рассматривать действия над всеми видами дробей и смешанными числами одновременно, причем эти преобразования не нарушают системы изучения действий, связаны с конкретными представлениями дробей и сводятся к дей­ствиям над целыми числами.

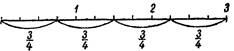
При рассмотрении различных долей единицы и дробей естественно поставить вопрос о сравнении их по величине, также кладется сравнение величин, измеряемых данными дробями. Для иллюстрации сравнительной величины долей единицы полезно на вы­бранной линейной единице от одного из ее концов отложить отрезки, соответствующие долям единицы (рис.7).

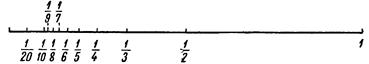
Рис.7

Для вывода формальных признаков сравнения дробей можно рекомендовать проводить работу по следующему плану: 1) сравнение долей единицы, 2) сравнение дробей с одинаковыми знаменателями, с одинаковыми числителями (не устанавливая, во сколько раз одна дробь больше другой), основное свойство дроби. Вывод основного свойства следует построить на том положении, что дроби, измеряющие одну и ту же величину при одной и той же единице измерения, равны. Таким образом, основное свойство получится как следствие определения равенства дробей, что соответствует научному построению изучения дробей. Следует при этом воспользоваться следующим наглядным пособием в виде таблицы:

Рис.8

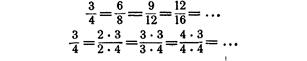
Для вывода основного свойства дроби в ряде учебников и ме­тодик предлагается предварительно изучить изменение величины дроби с увеличением (или уменьшением) числителя или знаменателя в несколько раз, причем устанавливается, во сколько раз увеличи­вается или уменьшается при этом дробь. Выводится правило увели­чения и уменьшения дроби в несколько раз, т. е. умножения и деления дроби на целое число. После этого рассматривается одно­временно увеличение (или уменьшение) членов дробей водно и то же число раз и устанавливается основное свойство дроби.

Рассмотрение увеличения или уменьшения дроби в несколько раз следует увязывать с прохождением умножения и деления дроби на целое число, так как эти задачи тождественны. Если же этот вопрос рассматривать до действий, то необходимо показать, что, увеличивая дробь в несколько раз, мы ее умножаем на целое число, уменьшая - делим на целое число, но тогда нарушится систематичность изложе­ния. Очень часто эта связь не подчеркивается, и учащиеся не осознают тождественность задач — увеличить дробь в несколько раз и умножить дробь на целое число, и не решаются применять правила увеличения и уменьшения дроби при умножении и делении дроби на целое число. Такое изучение увеличения и уменьшения дроби в несколько раз приносит вред учащимся, создавая путаницу в их умах.

После этого следует перейти к преобразованиям дробей: к со­кращению дробей, затем к приведению дробей к общему знамена­телю, связав это преобразование с задачей сравнения дробей с раз­ными числителями и знаменателями.

Для сознательного усвоения преобразования дробей следует привести чертеж. Например, сокращение дроби можно показать следующим образом:

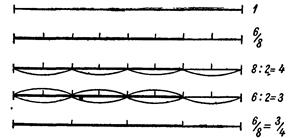
Рис.9

При этом ведутся следующие рассуждения: возьмем отрезок, составляющий линейной единицы; 8 восьмых долей единицы можно сгруппировать по 2 восьмых, тогда число долей, на которые разделена единица, уменьшится в 2 раза (8:2=4), 6 восьмых долей то же единицы тоже можно сгруппировать по 2 восьмых, тогда тело долей в данном отрезке тоже уменьшится в 2 раза (6:2=3);

отрезок, составленный из 6 восьмых линейной единицы, можно рассматривать составленным из 3 четвертей той же единицы.

Действия над дробями

Сложение и вычитание дробей

Изучение темы следует начать со сложения дробей с одинаковыми знаменателями и на конкретных примерах подчеркнуть, что сложение дробей состоит в подсчете одинаковых долей, содержащихся в данных дробях вместе, т. е. определение сложения дробей мало отличается от определения сложения чисел.

При сложении дробей с одинаковыми знаменателями следует составить систему упражнений, охватывающую все возможные случаи сложения: 1) целого с дробью; 2) целого со смешанным числом; 3) двух правильных дробей: а) дающих, в сумме правильную дробь, б) дающих в сумме целое число, в) дающих в сумме неправильную дробь; 4) смешанного числа с дробью, причем сумма дробей - правильная дробь; 5) то же, только сумма дробей - целое число;

6) то же, только сумма дробей — неправильная дробь; 7), 8), 9) те же случаи для суммы смешанных чисел. При сложении дробей с раз­ными знаменателями в основу системы упражнений берутся различ­ные случаи отыскания общего знаменателя. Следует вначале брать простые случаи отыскания общего знаменателя, которые не отвлекали бы от основной задачи — сложения дробей. На основании рассмотрения различных примеров следует добиться, чтобы учащиеся установили справедливость законов сложения для дробных чисел. Например:

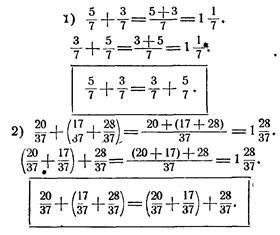
Рассуждения, приведенные на частных примерах, имеют общий характер, а именно: сложение дробей с одинаковыми знаменателями сводится к сложению числителей, т. е. целых чисел; так как для целых чисел справедливы законы сложения, следовательно, они спра­ведливы и для дробных чисел.

Вычитание дробей определяется, так же как и для целых чисел, как действие, обратное сложению.

Некоторые авторы предлагают проходить вычитание параллельно с сложением. Такой порядок имеет свои пре­имущества; этим самым все время подчеркивается связь вычитания с сложением как действия, обратного сложению. Большинство же учебников и задачников сначала рассматривают сложение дробей, потом вычитание, после этого — совместно сложение и вычитание, считая, что последний порядок изучения сосредоточивает внимание учащихся на одной трудности.

При вычитании дробей система упражнений имеет еще большее значение, чем при сложении, так как при вычитания иногда прихо­дится уменьшаемое преобразовывать, что затрудняет учащихся. Посте­пенно усложняя упражнения, можно подготовить учащихся к усвое­нию трудных случаев вычитания. Рассмотрим различные случаи, которые могут быть положены в основу системы упражнений на вычитание дробей с одинаковыми знаменателями, а именно: 1) из дроби вычесть дробь; 2) из смешанного числа - дробь, которая меньше дроби смешанного числа; 3) из единицы - дробь; 4) из це­лого числа, большего единицы, - дробь; 5) из числа, равного еди­нице с дробью, вычесть дробь, которая больше дроби в уменьшае­мом; 6) из смешанного числа - смешанное, причем дробь вычитае­мого меньше дроби уменьшаемого; 7) из целого - смешанное число; 8) из смешанного - смешанное число дробь которого больше дроби уменьшаемом. Примерная запись при сложении и вычитании дробей.

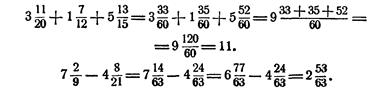
Не следует спешить переходить к записи общего знаменателя |вод одной чертой; учащиеся часто не осознают, что производится рамена данных дробей им равными дробями с общим знаменателем.

Умножение дроби на целое число