Реферат: Многомерные последовательности Фибоначчи

2. Любая аддитивная тройка со взаимно простыми компонентами входит в трёхмерную последовательность Фибоначчи, причём ровно один раз.

Доказательство (Теорема 1). Посчитаем наибольший общий делитель любых двух чисел в такой тройке. По алгоритму Евклида, он равен наибольшему общему делителю в предыдущей аддитивной тройке, из которой была образована данная. Так как все такие тройки, в конечном итоге, образуются из простейших троек, в которых любые два числа взаимно просты, то в любой тройке все числа попарно взаимно просты. Теорема доказана.

Доказательство (Теорема 2). Разобьём теорему на два утверждения. Первое утверждение: «Никакая тройка в последовательности не встретится дважды». Второе утверждение: «Любая аддитивная тройка со взаимно простыми компонентами входит в трёхмерную последовательность Фибоначчи».

Обозначим за отношение между двумя числами, сумма которых образует третье число аддитивной тройки (для удобства отношения можно брать циклически, например, если сумма стоит на втором месте в тройке, то берётся отношение третьего числа к первому; а если сумма стоит на первом месте, то рассматривается отношение второго числа к третьему). Так как числа аддитивной тройки попарно взаимно просты, то λ можно считать несократимой дробью. Для конкретной тройки M_a [b] известен номер множества, в котором она содержится, значит, можно сказать, на каком месте в тройке стоит сумма. Следовательно (так как числа взаимно просты), из несократимой дроби можно восстановить исходную тройку. Поэтому далее вместо аддитивных троек мы для удобства доказательства будем писать лишь число λ. Ясно, что если было выписано число λ, то в более нижних рядах будут выписаны числа и . Теперь докажем исходные утверждения. Понятно, что производная «первым способом», то есть f(λ) даёт тройку (), а вторым способом, то есть g(λ), даёт тройку (). Зная такое число, можно определить (с учётом приведенных неравенств), с помощью какой производной оно было образовано. Действительно, если λ<1, то она образована с помощью первой производной, если λ>1, то с помощью второй. Если λ=1, то эта тройка – простейшая. Итак, для каждой аддитивной тройки мы однозначно восстанавливаем её первообразные вплоть до простейшей тройки. Если бы встретились две одинаковые тройки, то они, с учётом приведенных рассуждений, были бы образованы от одной простейшей, и стояли бы в одном множестве, а значит, совпадали. Поэтому такое невозможно. Первое утверждение доказано. С другой стороны, чтобы доказать второе утверждение, достаточно рассмотреть произвольную дробь и показать, что с помощью приведенных выше преобразований можно получить эту дробь из единицы. Это нетрудно сделать, используя алгоритм Евклида. Если дробь больше единицы, отнимем от неё единицу. Если меньше, то разделим единицу на эту дробь. Так как числа в дроби взаимно просты, то бесконечно такие преобразования выполнять нельзя, поэтому рано или поздно мы придём к единице, а значит, такое число (и соответствующая ему аддитивная тройка) будет содержаться в 3-х мерной последовательности Фибоначчи.

Теорема доказана.

2. Упорядочивание, вычисление элементов последовательности

Упорядочим элементы каждого множества следующим образом:

Для начала, i-тый элемент множества M_k будем обозначать М_k [i].

В первом множестве находится единственная аддитивная тройка: М₁ [1]= =(2,1,1).

f(М_a [b]) = M_{a +1} [b] (Первая производная от аддитивной тройки М_a [b] лежит в следующем множестве, но индекс аддитивной тройки сохраняется.)

g(M_a [b]) = M_{a +2} [b+|M_{a +1} |] (Вторая производная от аддитивной тройки лежит в множестве «через одно», индекс увеличивается на количество элементов в множестве М_{a +1} .)

Изобразим это схематически (каждая аддитивная тройка обозначена точкой).

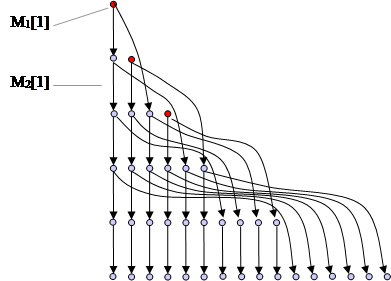Итак, мы занумеровали, то есть упорядочили элементы каждого множества М_i . Определим для всех a и b, для которых определена аддитивная тройка М_a [b], все три её элемента.

Для начала найдём все тройки вида M_a [1] (тройки первого столбца). Вычисляя результаты первых троек, замечаем общую закономерность и вычисляем общий вид.

M1 [1] = (2, 1, 1) = (F3 , F1 , F2 )	M3k+1 [1] = (F3k+3 , F3k+1 , F3k+2 )
M2 [1] = (2, 3, 1) = (F3 , F4 , F2 )	M3k+2 [1] = (F3k+3 , F3k+4 , F3k+2 )
M3 [1] = (2, 3, 5) = (F3 , F4 , F5 )	M3k [1] = (F3k , F3k+1 , F3k+2 )

Заметим, что если требуется вычислить некоторое число из обычной последовательности Фибоначчи, возможно, с изменёнными первыми членами, то для этого идеально подходит характеристический многочлен. Таким образом, все аддитивные тройки первого столбца можно вычислить в общем виде.

3. Некоторые зависимости между мнимыми тройками

Теперь расширим понятие M_a [b]. Определим её для всех целых a. Для этого введём понятие «первообразной».

Первообразной от аддитивной тройки Т₁ назовём такую аддитивную тройку Т₀ , что производная первым способом от неё равна аддитивной тройке Т₁ . При этом стоит отметить, что не каждая первообразная является натуральной тройкой, то есть не все числа в первообразной натуральны.

Первообразные от троек считаются по следующему правилу:

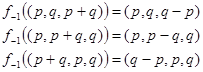
Аналогичным образом можно определить «N раз производную» и «N раз первообразную» - это композиции N подряд идущих функций либо f, либо g, либо f_-1. Поместим первообразную от аддитивной тройки M_a [b] во множество M_{a -1} ,

то есть f_-1 (M_a [b])=M_{a -1} [b]. Таким образом, многомерная последовательность Фибоначчи определена M_a [b] для всех целых b.

Теперь полученную 3х-мерную последовательность Фибоначчи можно изобразить так: