Реферат: Многомерные последовательности Фибоначчи

Итак, определены все аддитивные тройки M_a [b], где b – натуральное, a целое. В частности, рассмотрим аддитивные тройки вида M₁ [i], то есть тройки, находящиеся в первом ряду.

Каждая такая аддитивная тройка имеет вид (x_i +y_i , x_i , y_i ) и определяется двумя числами: x_i и y_i .

Рассмотрим последовательность Фибоначчи, в которой первые два числа равны соответственно x_i и y_i , а каждое число, начиная с третьего по-прежнему равняется сумме двух предыдущих. Зная числа x_i , y_i i-того столбца можно вычислить все аддитивные тройки в этом столбце, по аналогии с первым столбцом.

Итак, имеют место следующие равенства:

M3k+1 [i]=(F3k+3 , F3k+1 , F3k+2 )	M1 [i]=(xi +yi , xi , yi )
M3 k +2 [i]=(F3 k +3 , F3 k +4 , F3 k +2 )	F1 =xi , F2 =yi
M3 k [i]=(F3 k , F3 k +1 , F3 k +2 )	Fn +2 =Fn +1 + Fn

Понятно, что если мы найдём первую аддитивную тройку некоторого столбца, то сможем вычислить и все остальные тройки этого столбца. Ниже записаны первые тройки столбцов с номерами от 1 до 10.

M1[1]=(2, 1, 1)

M1[2]=(1, 0, 1)

M1[3]=(2, 3, -1)

M1[4]=(1, 1, 0)

M1[5]=(-2, -7, 5)

M1[6]=(-1, 4, 3)

M1[7]=(8, 19, -11)

M1[8]=(5, 12, -7)

M1[9]=(4, 9, -5)

M1[10]=(3, 7, -4)

Ниже изложен алгоритм по нахождению общего члена последовательности. Для начала определим ряд Фибоначчи для всех целых чисел. F_{- n} =(-1)^{n +1} F_n .

Далее определим формулу для «N раз производной» (эта же формула выполняется для «N раз первообразной»)

Пусть исходная тройка имеет вид:

Тогда её производные равны:

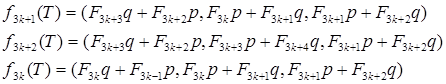
Теперь вычислим все элементы первой строки рекуррентно, но с маленьким числом действий.

Для начала заметим, что каждое число n большее 4 лежит между двумя удвоенными числами Фибоначчи. (2F_{i -1} n2F_i ) Каждому n поставим в соответствие номер i и назовём это «обратной функцией Фибоначчи» для n. Где это используется при решении задачи? Оказывается, такая «обратная функция» от n указывает на номер строки, в которой первый раз для данного столбца встречается натуральная тройка. Действительно, количество элементов каждой строки (кроме первой) равняется удвоенному соответствующему числу Фибоначчи. Назовём такую обратную функцию l_F (N).

Теперь, опускаясь из тройки первого столбца в первую натуральную тройку, и далее поднимаясь по стрелке (так как такая тройка всегда образована с помощью производной «вторым способом»), нетрудно проверить справедливость следующей формулы:

Например,

Наряду с общей формулой, для всех натуральных троек верна более простая, рекуррентная, которая следует из определения (эта формула для мнимых троек, вообще говоря, не выполняется):