Реферат: Многомерные последовательности Фибоначчи

Для начала выпишем таблицу, содержащую некоторые тройки не в схематическом, а в непосредственном виде. (см. приложение)

Если брать производные вторым способом от мнимых троек, можно заметить следующие закономерности (для некоторых троек), например:

f-₂ (g(T))=g_-1 (f₂ (T))

g(f_-3 (g(T)))=-f(g(f(T)))

Их можно доказать, используя определение производных и первообразных. Докажем утверждение для тройки 1 рода (аналогичное утверждение для остальных получается циклическим сдвигом компонент)

1. f-₂ (g(T))=g_-1 (f₂ (T))

(p + q , p, q) ->(f)->(p+q, p +2 q , q) ->(f)->(p+q, p+2q, 2 p +3 q )->(g_-1 )->(p + q , p+2q, -q)

(p + q , p, q) ->(g)->(p+q, p, 2 p + q ) ->(f_-1 )->(p+q, p , -q) -> (f_-1 )-> (p + q , p+2q, -q)

Так как конечные результаты преобразований верны для любых чисел p, q, то утверждение верно для любых троек Т. Аналогично доказывается второе утверждение.

2.g(f_-3 (g(T)))=-f(g(f(T)))

(p + q , p, q) ->(g)->(p+q, p, 2p+q) -> (f_-1 ) –> (p+q, p, -q) -> (f_-1 ) -> (p+q, p+2q, -q) -> (f_-1 ) ->

-> (-p-3q, p+2q, -q) ->(g) -> (-p-3q, -p-4q, -q) = -(p+3q, p+4q, q)

(p+1,p,q)-> (f) -> (p+q, p+2q, q) -> (g) -> (p+3q, p+2q, q) -> (f) -> (p+3q, p+4q, q)

Далее исследуем условия, необходимые и достаточные для существования аддитивной тройки в трёхмерной последовательности Фибоначчи.

Лемма. Если тройка (a,b,c) находится в трёхмерной последовательности Фибоначчи, то хотя бы одно из чисел a,b,c положительно.

Доказательство. Допустим, что в данной тройке все компоненты отрицательны. Ясно, что если тройка содержится в последовательности, то строя производные от неё (первым способом), мы рано или поздно получим тройку со всеми натуральными компонентами. Но если брать производные от тройки с неположительными компонентами, то будут получаться только тройки с неположительными компонентами. Противоречие. Лемма доказана.

Примечание. Все приведенные ниже теоремы верны для циклического сдвига компонент троек.

Теорема

Пусть p,q – натуральные взаимно простые числа. Тогда верны следующие утверждения.

а) тройка (p+q, p, -q)=T всегда находится в трёхмерной последовательности Фибоначчи.

б) тройка (p+q, -p, q)=T находится в последовательности тогда и только тогда, когда ( - золотое сечение, )

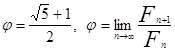в) тройка (-p-q, p, -q)=T находится в последовательности тогда и только тогда, когда

г) тройка (-p-q, -p, q)=Tне находится в трёхмерной последовательности Фибоначчи.

Доказательство.

а) Возьмём производную от тройки, первым способом. Получим:

f(p+q, p, -q)=(p+q, p, 2p+q). То есть раз мы получили натуральную тройку, то исходная тройка действительно содержится в исходной последовательности.

г) Аналогично, возьмём производную. f(-p-q, -p, q)=(-p-q, -p, -2p-q). Получена тройка с отрицательными компонентами, а по лемме, приведенной в начале главы, такой тройки не содержится в последовательности, значит, исходная тройка в последовательности также не содержится.

в) Строя последовательно производные, получаем тройки, каждая компонента которых имеет вид F_n q-F_{n +1} p. Так как в конечном итоге каждая компонента должна стать больше нуля, то неравенство F_n q-F_{n +1} p>0 должно выполняться для всех n>M для некоторого M. При n стремящемся к бесконечности получаем , или

б) Аналогично получаем (умножая все числа в пункте в. на минус один), что каждая компонента имеет вид -F_n q+F_{n +1} p>0, и .